Source

Parameter Space - 1D¶

I've broken down the components so that it's easier to pass appropriate parameters. The main functions as as follows:

Standardize Data
- yes or no
Get Sigma
- Handles the ways to estimate the parameter
- per dimension
- per dataset (x and/or y)
- estimator (median, mean, silverman, scott, etc)
Get HSIC scorer
- Handles the HSIC method (hsic, ka, cka)

Code Blocks

Imports

import sys, os

# Insert path to model directory,.
cwd = os.getcwd()
path = f"{cwd}/../../src"
sys.path.insert(0, path)

# Insert path to package,.
pysim_path = f"/home/emmanuel/code/pysim/"
sys.path.insert(0, pysim_path)

import warnings
from tqdm import tqdm
import random
import pandas as pd
import numpy as np
import argparse
from sklearn.utils import check_random_state

# toy datasets
from data.toy import generate_dependence_data
from data.distribution import DataParams
from features.utils import dict_product


# Kernel Dependency measure
from sklearn.gaussian_process.kernels import RBF
from pysim.kernel.hsic import HSIC
from pysim.kernel.utils import estimate_sigma, get_sigma_grid#GammaParam, SigmaParam

# RBIG IT measures
from models.dependence import HSICModel

# Plotting
from visualization.distribution import plot_scorer

# experiment helpers
from tqdm import tqdm
from experiments.utils import dict_product, run_parallel_step

# Plotting Procedures
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use(['seaborn-paper'])
warnings.filterwarnings('ignore') # get rid of annoying warnings
%matplotlib inline

%load_ext autoreload
%autoreload 2

Standardize Data

from typing import Optional, Tuple

def standardize_data(
    X: np.ndarray, 
    Y: np.ndarray, 
    standardize: bool=False
) -> Tuple[np.ndarray, np.ndarray]:
    X = StandardScaler().fit_transform(X)
    Y = StandardScaler().fit_transform(Y)
    return X, Y

Estimate Sigma

def get_sigma(
    X: np.ndarray, 
    Y: np.ndarray, 
    method: str='silverman', 
    percent: Optional[float]=None,
    per_dimension: bool=False, 
    separate_scales: bool=False
) -> Tuple[np.ndarray, np.ndarray]:
    # sigma parameters
    subsample = None
    random_state = 123

    sigma_X = estimate_sigma(
        X, 
        subsample=subsample,
        method=method,
        percent=percent,
        random_state=random_state,
        per_dimension=per_dimension
    )

    sigma_Y = estimate_sigma(
        Y, 
        subsample=subsample,
        method=method,
        percent=percent,
        random_state=random_state,
        per_dimension=per_dimension
    )

    if separate_scales:
        sigma_X = np.mean([sigma_X, sigma_Y])
        sigma_Y = np.mean([sigma_X, sigma_Y])
    return sigma_X, sigma_Y

HSIC

def get_hsic(
    X: np.ndarray, 
    Y: np.ndarray, 
    scorer: str, 
    sigma_X: Optional[float]=None, 
    sigma_Y: Optional[float]=None
) -> float:

    # init hsic model class

    hsic_model = HSICModel()
    # hsic model params
    if sigma_X is not None:

        hsic_model.kernel_X = RBF(sigma_X)
        hsic_model.kernel_Y = RBF(sigma_Y)

    # get hsic score
    hsic_val = hsic_model.get_score(X, Y, scorer)

    return hsic_val

def plot_toy_data(X, Y, subsample: Optional[int]=None):

    # plot
    fig, ax = plt.subplots()

    ax.scatter(X[:subsample,:], Y[:subsample,:])
    return fig, ax

Datasets¶

For this experiment, we will be looking at 4 simple 1D datasets:

Line
Sine
Circle
Random

Code Block

datasets = ['line', 'sine', 'circle', 'random']
num_points = 1_000
seed = 123
noise = 0.1

for idataset in datasets:
    # get dataset
    X, Y = generate_dependence_data(
        dataset=idataset,
        num_points=num_points,
        seed=seed,
        noise_x=noise,
        noise_y=noise
    )

    fig, ax = plot_toy_data(X, Y, 100)
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
    plt.tight_layout()
    fig.savefig(FIG_PATH + f"demo_{idataset}.png")
    plt.show()

png

Research Questions¶

Which Algorithm?
Which Parameter Estimator?
Standardize or Not?

Part I - The Sigma Space¶

Experiment¶

For this first part, we want to look a the entire $\sigma$ space for the RBF kernel. We will vary the $\sigma$ parameter and use 20 grid poinnts for both $X$ and $Y$ . Since we're dealing with 1D data, we will not have to worry about per dimension estimates.

Free Parameters

Dataset (sine, line, circle, random)
Scorer (hsic, cka, ka)
Sigma X,Y (grid space)

We fix all other parameters as they are not necessary for this first step.

Code Blocks

Sigma Grid

def sigma_grid(sigma_X, factor=2, n_grid_points=20):
    return np.logspace(
        np.log10(sigma_X * 10**(-factor)),
        np.log10(sigma_X * 10**(factor)),
        n_grid_points
    )

Experimental Params

This made a list of dictionary values with every possible combination of the parameters we listed. Now if we call the first element of this list, we can pass these parameters into our HSIC function to calculate the score. This allows us to do the calculations in parallel instead of looping through every single combination.

# experimental parameters
n_grid_points = 40
# sigma_grid = np.logspace(-3, 3, n_grid_points)

# initialize sigma (use the median)
sigma_X, sigma_Y = get_sigma(X,Y, method='mean')
print(sigma_X, sigma_Y)

# create a grid
sigma_X_grid = sigma_grid(sigma_X, factor=3, n_grid_points=n_grid_points)
sigma_Y_grid = sigma_grid(sigma_Y, factor=3, n_grid_points=n_grid_points)

# create a parameter grid
parameters = {
    "dataset": ['sine', 'line', 'random', 'circle'],
    "scorer": ['hsic', 'ka', 'cka'],
    "sigma_X": np.copy(sigma_X_grid),
    "sigma_Y": np.copy(sigma_Y_grid),
}

# Get a list of all parameters
parameters = list(dict_product(parameters))

# check # of parameters
n_params = len(parameters)
print(f"Number of params: {n_params}")
print(f"First set of params:\n{parameters[0]}")

0.32917944341805494 0.3439255265652333
Number of params: 19200
First set of params:
{'dataset': 'sine', 'scorer': 'hsic', 'sigma_X': 0.00032917944341805485, 'sigma_Y': 0.00034392552656523323}

Experimental Step

Now, we need to make an experimental step function. This function will be the HSIC function that called within the parallel loop. I want it to also return a pd.DataFrame with the columns holding the parameters. This will make things easier for us to keep track of things as well as plot our results.

from typing import Dict

def step(params: Dict, X: np.ndarray, Y: np.ndarray)-> pd.DataFrame:

    # get dataset
    X, Y = generate_dependence_data(
        dataset=params['dataset'],
        num_points=1_000,
        seed=123,
        noise_x=0.1,
        noise_y=0.1
    )

    # calculate the hsic value
    score = get_hsic(X, Y, params['scorer'], params['sigma_X'], params['sigma_Y'])

    # create a dataframe with the results and params
    results_df = pd.DataFrame({
        'dataset': [params['dataset']],
        'scorer': [params['scorer']],
        'sigma_X': [params['sigma_X']],
        'sigma_Y': [params['sigma_Y']],
        'score': score,
    },)

    return results_df

Example

Now we can loop through and calculate the hsic value for each of the $\sigma$ -parameters that we have enlisted. And we will do it in parallel to save time. I'm on a server with 28 cores free so best believe I will be using all of them...

# test the result
res_test = step(parameters[0], X, Y)

# quick test
res_keys = ['dataset', 'scorer', 'sigma_X', 'sigma_Y', 'score']
assert res_keys == res_test.columns.tolist()

# print out results
res_test.head().to_markdown()

	dataset	scorer	sigma_X	sigma_Y	score
0	sine	hsic	0.000329179	0.000343926	0.000997738

Experiment

verbose = 1
n_jobs = -1

results = run_parallel_step(
    exp_step=step, 
    parameters=parameters,
    n_jobs=n_jobs,
    verbose=verbose,
    X=X,
    Y=Y
)

[Parallel(n_jobs=-1)]: Using backend LokyBackend with 28 concurrent workers.
[Parallel(n_jobs=-1)]: Done 232 tasks      | elapsed:    2.0s
[Parallel(n_jobs=-1)]: Done 732 tasks      | elapsed:    5.6s
[Parallel(n_jobs=-1)]: Done 1432 tasks      | elapsed:   10.5s
[Parallel(n_jobs=-1)]: Done 2332 tasks      | elapsed:   15.1s
[Parallel(n_jobs=-1)]: Done 3432 tasks      | elapsed:   20.7s
[Parallel(n_jobs=-1)]: Done 4732 tasks      | elapsed:   29.9s
[Parallel(n_jobs=-1)]: Done 6232 tasks      | elapsed:   40.6s
[Parallel(n_jobs=-1)]: Done 7932 tasks      | elapsed:   48.7s
[Parallel(n_jobs=-1)]: Done 9832 tasks      | elapsed:  1.0min
[Parallel(n_jobs=-1)]: Done 11932 tasks      | elapsed:  1.2min
[Parallel(n_jobs=-1)]: Done 14232 tasks      | elapsed:  1.5min
[Parallel(n_jobs=-1)]: Done 16732 tasks      | elapsed:  1.8min
[Parallel(n_jobs=-1)]: Done 19145 out of 19200 | elapsed:  2.0min remaining:    0.3s
[Parallel(n_jobs=-1)]: Done 19200 out of 19200 | elapsed:  2.0min finished

# test (number of results = n parameters)
assert n_params == len(results)

results_df = pd.concat(results, ignore_index=True)
results_df.head().to_markdown()

	dataset	scorer	sigma_X	sigma_Y	score
0	sine	hsic	0.000329179	0.000343926	0.000997738
1	sine	hsic	0.000329179	0.000490129	0.000997927
2	sine	hsic	0.000329179	0.000698484	0.000998668
3	sine	hsic	0.000329179	0.000995412	0.000999668
4	sine	hsic	0.000329179	0.00141856	0.00100054

Part II - Specific Methods¶

In the above section, we showed the full parameter space. But what happens if we just look at specific ways to estimate the sigma? For th

Free Parameters:

Dataset (sine, line, circle, random)
Scorer (hsic, cka, ka)
Sigma Estimator (mean, median, silverman, scott)

Experiment¶

Code Block

# initialize sigma (use the median)
sigma_X, sigma_Y = get_sigma(X,Y, method='mean')

# create a parameter grid
parameters = {
    "dataset": ['sine', 'line', 'random', 'circle'],
    "scorer": ['hsic', 'ka', 'cka'],
    "estimator": ['mean', 'median', 'mean']
}

# Get a list of all parameters
parameters = list(dict_product(parameters))

# check # of parameters
n_params = len(parameters)
print(f"Number of params: {n_params}")
print(f"First set of params:\n{parameters[0]}")

Number of params: 36
First set of params:
{'dataset': 'sine', 'scorer': 'hsic', 'estimator': 'mean'}

from typing import Dict

def step(params: Dict, X: np.ndarray, Y: np.ndarray)-> pd.DataFrame:

    # get dataset
    X, Y = generate_dependence_data(
        dataset=params['dataset'],
        num_points=1_000,
        seed=123,
        noise_x=0.1,
        noise_y=0.1
    )
    # estimate sigma
    sigma_X, sigma_Y = get_sigma(X, Y, method=params['estimator'])

    # calculate the hsic value
    score = get_hsic(X, Y, params['scorer'], sigma_X, sigma_Y)

    # create a dataframe with the results and params
    results_df = pd.DataFrame({
        'dataset': [params['dataset']],
        'scorer': [params['scorer']],
        'estimator': [params['estimator']],
        'sigma_X': [sigma_X],
        'sigma_Y': [sigma_Y],
        'score': score,
    },)

    return results_df

# test the result
res_test = step(parameters[0], X, Y)

# quick test
res_keys = ['dataset', 'scorer', 'estimator', 'sigma_X', 'sigma_Y', 'score']
assert res_keys == res_test.columns.tolist(), f'Not true:{res_test.columns.tolist()}'

# print out results
res_test.head().to_markdown()

	dataset	scorer	estimator	sigma_X	sigma_Y	score
0	sine	hsic	mean	0.329179	0.820625	0.0661783

verbose = 1
n_jobs = 1

results = run_parallel_step(
    exp_step=step, 
    parameters=parameters,
    n_jobs=n_jobs,
    verbose=verbose,
    X=X,
    Y=Y
)

[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done  36 out of  36 | elapsed:    4.3s finished

# test (number of results = n parameters)
assert n_params == len(results)

results_est_df = pd.concat(results, ignore_index=True)
results_est_df.head().to_markdown()

	dataset	scorer	estimator	sigma_X	sigma_Y	score
0	sine	hsic	mean	0.329179	0.820625	0.0661783
1	sine	hsic	median	0.289021	0.72562	0.0770415
2	sine	hsic	mean	0.329179	0.820625	0.0661783
3	sine	ka	mean	0.329179	0.820625	0.91219
4	sine	ka	median	0.289021	0.72562	0.896967

Visualization - HeatMaps¶

Code Block

def plot_all_params(
    grid_df: pd.DataFrame, 
    params_df: Optional[pd.DataFrame]=None,
    scorer: str='hsc', 
    dataset: str='sine', 
):

    fig, ax = plt.subplots(figsize=(6, 5))

    # ===========================================
    # Plot Gridded DataFrame
    # ===========================================


    # subset hsic method
    grid_df_ = grid_df[grid_df['scorer'] == scorer].drop('scorer', axis=1)

    # subset dataset
    grid_df_ = grid_df_[grid_df_['dataset'] == dataset].drop('dataset', axis=1)

    # create a heatmap
    grid_df_ = pd.pivot_table(grid_df_, values='score', index=['sigma_Y'], columns='sigma_X')
#     print(grid_df_)
    # min max
    if scorer == 'hsic':
        vmax = 0.11
        vmin = grid_df_.values.min()
    else:
        vmax = 1.0
        vmin = grid_df_.values.min()
#     print(vmin)

    # heatmap_data.columns = np.sqrt(1 / 2 * heatmap_data.columns.values)
    # heatmap_data.index = np.sqrt(1 / 2 * heatmap_data.index.values)
    X, Y = np.meshgrid(grid_df_.index.values, grid_df_.columns.values, )
    pts = ax.pcolormesh(
        X, Y, grid_df_.values, #vmin=0, vmax=vmax, 
        cmap='Reds',vmin=0, vmax=vmax,
#         norm=colors.LogNorm(vmin=vmin, vmax=vmax)
    )

    # colorbar
    fig.colorbar(pts, ax=ax)
#     ax = sns.heatmap(
#         data=grid_df_,
#         xticklabels=grid_df_.columns.values.round(decimals=2),
#         yticklabels=grid_df_.index.values.round(decimals=2),
#         vmin=0, vmax=vmax
#     )
    # ===========================================
    # Plot Params
    # ===========================================    
    if params_df is not None:
        params_df_ = params_df[params_df['dataset'] == dataset]

        # subset hsic method
        params_df_ = params_df_[params_df_['scorer'] == scorer]

        # plot X
        estimators = [
            ('median', 'black'),
            ('mean', 'green'),
            ('silverman', 'blue'),
            ('scott', 'red'),
        ]


        for iest, icolor in estimators:

            # Plot X
#             print(
#                 params_df_[params_df_['estimator'] == iest].sigma_X,
#                 params_df_[params_df_['estimator'] == iest].sigma_Y
#             )
            ax.scatter(
                params_df_[params_df_['estimator'] == iest].sigma_X, 
                params_df_[params_df_['estimator'] == iest].sigma_Y,
                s=500, c=icolor, label=f"{iest.capitalize()} X", zorder=3, marker='.')
            # Plot Y
# #             ax.scatter(
# #                 , 
# #                 params_df[params_df['estimator'] == iest].score,
# #                 s=300, c=icolor, label=f"{iest.capitalize()} Y", zorder=3, marker='.')
    ax.legend()
    return fig, ax

Line Dataset¶

Code Block

scorers = results_df['scorer'].unique().tolist()
idataset = 'line'

for iscorer in scorers:

    fig, ax = plot_all_params(results_df, results_est_df, scorer=iscorer, dataset=idataset)

    # ax.legend(ncol=1, fontsize=15)
    plt.xscale('log', basex=10)
    plt.yscale('log', basey=10)
    ax.set_xlabel(r'$\sigma_X$', fontsize=20)
    ax.set_ylabel(r'$\sigma_Y$', fontsize=20)
    ax.set_title(f'{iscorer.upper()} Score, {idataset.capitalize()}', fontsize=20)
    plt.tight_layout()
    plt.show()

HSIC

png

Kernel Alignment

png

Centered Kernel Alignment

png

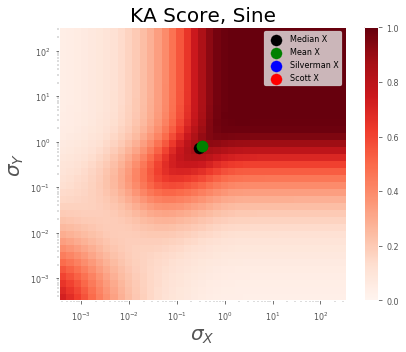
Sine Dataset¶

Code Block

scorers = results_df['scorer'].unique().tolist()
idataset = 'sine'

for iscorer in scorers:

    fig, ax = plot_all_params(results_df, results_est_df, scorer=iscorer, dataset=idataset)

    # ax.legend(ncol=1, fontsize=15)
    plt.xscale('log', basex=10)
    plt.yscale('log', basey=10)
    ax.set_xlabel(r'$\sigma_X$', fontsize=20)
    ax.set_ylabel(r'$\sigma_Y$', fontsize=20)
    ax.set_title(f'{iscorer.upper()} Score, {idataset.capitalize()}', fontsize=20)
    plt.tight_layout()
    plt.show()

HSIC

png

Kernel Alignment

![png](pics/param_grid/output_47_1.png)

Centered Kernel Alignment

png

Circle Dataset¶

Code Block

scorers = results_df['scorer'].unique().tolist()
idataset = 'circle'

for iscorer in scorers:

    fig, ax = plot_all_params(results_df, results_est_df, scorer=iscorer, dataset=idataset)

    # ax.legend(ncol=1, fontsize=15)
    plt.xscale('log', basex=10)
    plt.yscale('log', basey=10)
    ax.set_xlabel(r'$\sigma_X$', fontsize=20)
    ax.set_ylabel(r'$\sigma_Y$', fontsize=20)
    ax.set_title(f'{iscorer.upper()} Score, {idataset.capitalize()}', fontsize=20)
    plt.tight_layout()
    plt.show()

HSIC

png

Kernel Alignment

png

Centered Kernel Alignment

png

Random Dataset¶

Code Block

scorers = results_df['scorer'].unique().tolist()
idataset = 'random'

for iscorer in scorers:

    fig, ax = plot_all_params(results_df, results_est_df, scorer=iscorer, dataset=idataset)

    # ax.legend(ncol=1, fontsize=15)
    plt.xscale('log', basex=10)
    plt.yscale('log', basey=10)
    ax.set_xlabel(r'$\sigma_X$', fontsize=20)
    ax.set_ylabel(r'$\sigma_Y$', fontsize=20)
    ax.set_title(f'{iscorer.upper()} Score, {idataset.capitalize()}', fontsize=20)
    plt.tight_layout()
    plt.show()

HSIC

png

Kernel Alignment

png

Centered Kernel Alignment

png