Skip to article frontmatterSkip to article content
AI 4 Attribution

Extreme Value Modeling Evaluation

CSIC
UCM
IGEO

Empirical Fit

P-P Plot

Random image of the beach or ocean!

Figure 1:Example of p-p plot from wikipedia. [Source: Wikipedia]

This is also known as the probability-probability plot, the percent-percent plot, or the p-value plot. It is used for assessing how closely two datasets agree and/or the residuals. See wiki for more details.

Note: this plot only works when we have the theoretical cumulative distribution.

Q-Q Plot

Random image of the beach or ocean!

Figure 1:Example of Q-Q plot from wikipedia. [Source: Wikipedia]

This is the quantile-quantile plot. This is a graphical tool to compare two probability distributions by comparing their quantiles versus one another. See wiki for more details.

Predictions

Return Period

We can extrapolate an distribution by computing the pp-return level (see blog). This represents the high quantile for which the probability that the maximym exceeds this quantile is 1/p1/p. This concept is known as the return period. The return period of a particular event is the inverse probability that the event will be exceeded in any given year. For example, the pp-year return level is associated with a return period of pp years. The 1/p1/p return level is the 1−p1-p quantile of an arbitrary quantile function for a distribution.(Mahmoudian & Mahammadzadeh, 2014).

To compute the return level of ypy_p s.t. the distribution, Quantile(p)=1−p\text{Quantile}(p)=1-p. We can solve for pp which results in the following formula.

Distribution(yp)=1−pyp=Distribution−1(1−p)=Quantile(1−p) \begin{aligned} \text{Distribution}(y_p) &= 1 - p\\ y_p &= \text{Distribution}^{-1}(1-p)=\text{Quantile}(1-p) \end{aligned}
(1)
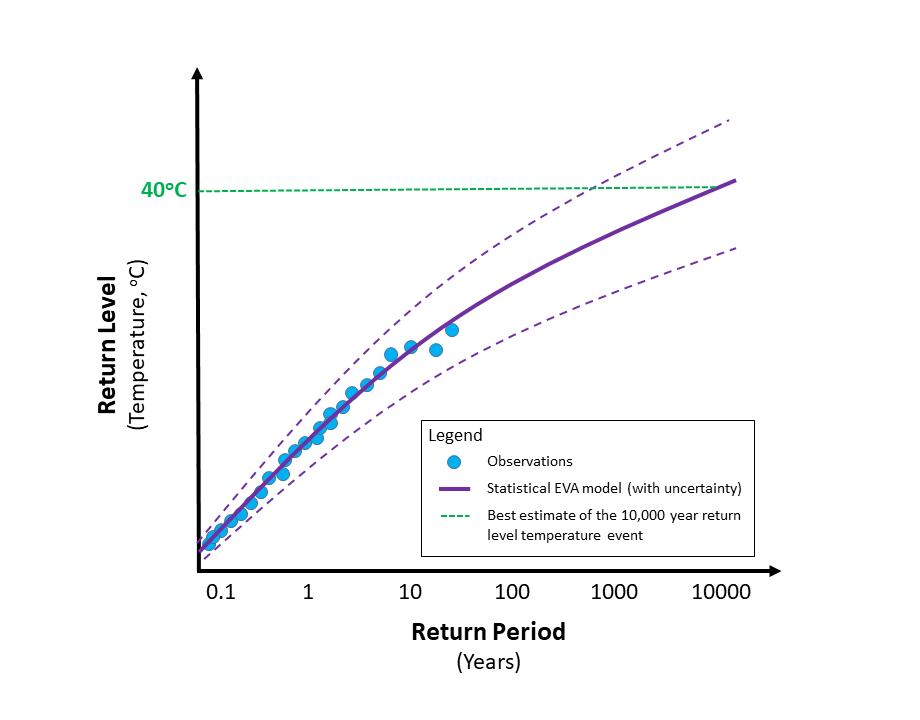
Random image of the beach or ocean!

Figure 1:Example of return period for temperature. [Source: MetOffice]

This is also known as the recurrence interval or repeat interval which is an average time or an estimated average time between events. In the case of extreme events, these can include floods, heatwaves, or droughts. See wiki for more details.

Interpretations

Waiting Time - The average waiting time until next occurrence of the event in tt years.

Number of Events - The average number of events occurring within a TT-year period.

Example: GEVD

The return period is a nifty tool for making predictions of along the tails of the distribution. We simply need the quantile function for the arbitrary distribution. The quantile function maps some input, uu, to a threshold value yy so that the probability of yy being less than or equal than yy is pp.

Q:[0,1]→R \text{Q}:[0,1] \rightarrow \mathbb{R}
(2)

We can an example for the GEVD. For the GEVD, we have the quantile function defined as

QGEVD(p;μ,σ,ξ)={μ−σξ[1−(−log⁡p)−ξ],ξ≠0μ−σlog⁡(−log⁡p),ξ=0 \text{Q}_{GEVD}(p;\mu,\sigma,\xi) = \begin{cases} \mu - \frac{\sigma}{\xi} \left[ 1 - \left( - \log p\right)^{-\xi} \right], && \xi \neq 0 \\ \mu - \sigma\log\left( - \log p\right), && \xi = 0 \end{cases}
(3)

One can easily find this function (along with many others) in a wiki or any similar resource. Now, we simply plug in the return level, i.e., 1−p1-p, into the quantile function

QGEVD(1−p;μ,σ,ξ){μ−σξ{1−[−log⁡(1−p)]−ξ},ξ≠0μ−σlog⁡{−log⁡(1−p)},ξ=0 \text{Q}_{GEVD}(1-p;\mu,\sigma,\xi) \begin{cases} \mu - \frac{\sigma}{\xi} \left\{ 1 - \left[ - \log(1-p)\right]^{-\xi} \right\}, && \xi \neq 0 \\ \mu - \sigma\log\left\{ - \log(1 - p)\right\}, && \xi = 0 \end{cases}
(4)
Example: GPD

The return period is a nifty tool for making predictions of along the tails of the distribution. We simply need the quantile function for the arbitrary distribution. The quantile function maps some input, uu, to a threshold value yy so that the probability of yy being less than or equal than yy is pp.

Q:[0,1]→R \text{Q}:[0,1] \rightarrow \mathbb{R}
(5)

We can an example for the GEVD. For the GPD, we have to be careful because we don’t have an exact expression.

QGPD(p;μ,σ,ξ)={μ−σξ[1−(−log⁡p)−ξ],ξ≠0u+σulog⁡(pξu)ξ=0 \text{Q}_{GPD}(p;\mu,\sigma,\xi) = \begin{cases} \mu - \frac{\sigma}{\xi} \left[ 1 - \left( - \log p\right)^{-\xi} \right], && \xi \neq 0 \\ u + \sigma_u \log \left(p\xi_u \right) && \xi = 0 \end{cases}
(6)

where ξu\xi_u is the probability of exceeding the threshold. We can use this to estimate the return level, ypy_p.

y^p=u+σ^uξ^[(npNu)−ξ^−1] \hat{y}_p = u + \frac{\hat{\sigma}_u}{\hat{\xi}} \left[ \left(\frac{np}{N_u}\right)^{-\hat{\xi}} - 1 \right]
(7)

Mean Excess Function

E(Y−u∣Y>u=σu−uξ1−ξ)\mathbb{E}(Y - u|Y>u = \frac{\sigma_u - u\xi}{1 - \xi})
(8)

where the scale parameter, σu\sigma_u, varies linearly in the threshold uu and the shape parameter ξ is fixed wrt the threshold uu.

Expected Shortfall

Ultimately, the goal of EVT is to compute the value at risk. We can derive the expected shortfall (conditional rv).

yp=μ−σξ[1−(NNμ(1−p))−ξ] y_p = \mu - \frac{\sigma}{\xi}\left[ 1 - \left(\frac{N}{N_\mu} (1 - p) \right)^{-\xi} \right]
(9)

where:

  • ypy_p - the random variable
  • μ - the threshold (in percentage terms)
  • NN - number of observations
  • NμN_\mu - # of observations that exceed the threshold

We can define the expected shortfall (ES) as:

ES=yp1−ξ+σ−ξμ1−ξ \text{ES} = \frac{y_p}{1 -\xi} + \frac{\sigma - \xi\mu}{1 - \xi}
(10)
References
  1. Mahmoudian, B., & Mohammadzadeh, M. (2014). A spatio-temporal dynamic regression model for extreme wind speeds. Extremes, 17(2), 221–245. 10.1007/s10687-014-0180-2
Basics
Calculating Extremes
Covariate Effects
II - Covariates Effects