Skip to content

Sparse Gaussian Processes

[toc]

Sparse GPs refer to a family of methods that seek to take a subset of points in order to approximate the full dataset. Typically we can break them down into 5 categories:

  • Subset of Data (Transformation, Random Sampling)
  • Data Approximation Methods (Nystrom, Random Fourer Features, Random Kitchen Sinks, Sparse-Spectrum, FastFood, A la Carte)
  • Inducing Points (SoR, FITC, DTC, KISS-GP)
  • Linear Algebra (Toeplitz, Kronecker, )
  • Approximate Inference (Variational Methods)

Each of these methods ultimately augment the model so that the largest computation goes from \mathcal{O}(N^3) to \mathcal{O}(MN^2) where M<<N.

Subset of Data

This is the simplest way to approximate the data. The absolute simplest way is to take a random subsample of your data. However this is often not a good idea because the more data you have the more information you're more likely to have. It's an age old rule that says if you want better predictions, it's often better just to have more data.

A more sophisticated way to get a subsample of your data is to do some sort of pairwise similarity comparison scheme - i.e. Kernel methods. There are a family of methods like the Nystrom approximation or Random Fourier Features (RFF) which takes a subset of the points through pairwise comparisons. These are kernel matrix approximations so we can transform our data from our data space \mathcal{X} \in \mathbb{R}^{N \times D} to subset data space \mathcal{Z} \in \mathbb{R}^{M \times d} which is found through an eigen decomposition scheme.

In GPs we calculate a kernel matrix \mathbf K \in \mathbb{R}^{N \times N}. If N is large enough, then throughout the marginal likelihood, we need to calculate \mathbf K^{-1} and |\mathbf K| which has \mathcal{O}(N^3) operations and \mathcal{O}(N^2) memory costs. So we make an approximate matrix \mathbf {\tilde{K}} given by the following formula:

\tilde{K}=K_{z}K_{zz}^{-1}K_z^{\top}

where: * K_{zz}=K(z,z)\in \mathbb{R}^{M\times M} - the kernel matrix for the subspace \mathcal{Z} * K_z=K(x,z)\in \mathbb{R}^{N\times M} - the transformation matrix from the data space \mathcal{X} to the subspace \mathcal{Z} * K \approx \tilde{K} \in \mathbb{R}^{N \times N} - the approximate kernel matrix of the data space \mathcal{X}

Below is an example of where this would be applicable where we just implement this method where we just transform the day.

from sklearn.kernel_approximation import Nystroem
from sklearn.gaussian_process import GaussianProcessRegressor as GPR
from sklearn.gaussian_processes.kernels import RBF

# Initialize Nystrom transform
nystrom_map = Nystrom(
    random_state=1,
    n_components=1
)

# Transform Data
X_transformed = nystrom_map.fit_transform(X)

# initialize GPR
model = GPR()

# fit GP model
model.fit(X_transformed, y)

Kernel Approximations

Pivoting off of the method above, we So now when we calculate the log likelihood term \log \mathcal{P}(y|X,\theta) we can have an approximation:

\log \mathcal{N}(y | 0, K + \sigma^2I) \approx \log \mathcal{N}(y | 0, \tilde{K} + \sigma^2I)

Notice how we haven't actually changing our formulation because we still have to calculate the inverse of \tilde{K} which is \mathbb{R}^{N \times N}. Using the Woodbury matrix identity for the kernel approximation form (Sherman-Morrison Formula):

(\tilde{K} + \sigma^2 I)^{-1}=\sigma^{-2}I - \sigma^{-4}K_z(K_{zz}+\sigma^{-2}K_z^{\top}K_z)^{-1}K_z^{\top}

Now the matrix that we need to invert is (K_{zz}+\sigma^{-2}K_z^{\top}K_z)^{-1} which is (M \times M) which is considerably smaller if M << N. So the overall computational complexity reduces to \mathcal{O}(NM^2).

Inducing Points

Sparse GPs - Inducing Points Summary

So I think it is important to make note of the similarities between methods; specifically between FITC and VFE which are some staple methods one would use to scale GPs naively. Not only is it helpful for understanding the connection between all of the methods but it also helps with programming and seeing where each method differs algorithmically. Each sparse method is a method of using some set of inducing points or subset of data \mathcal{Z} from the data space \mathcal{D}. We typically have some approximate matrix \mathbf{Q} which approximates the kernel matrix \mathbf{K}:

\mathbf{Q}_{ff}=\mathbf{K}_{fu}\mathbf{K}_{uu}^{-1}\mathbf{K}_{uf}

Then we would use the Sherman-Morrison formula to reduce the computation cost of inverting the matrix \mathbf{K}. Below is the negative marginal log likelihood cost function that is minimized where we can see the each term broken down:

\mathcal{L}(\theta)= \frac{N}{2}\log 2\pi + \underbrace{\frac{1}{2} \log\left| \mathbf{Q}_{ff}+G\right|}_{\text{Complexity Penalty}} + \underbrace{\frac{1}{2}\mathbf{y}^{\top}(\mathbf{Q}_{ff}+G)^{-1}\mathbf{y}}_{\text{Data Fit}} + \underbrace{\frac{1}{2\sigma_n^2}\text{tr}(\mathbf{T})}_{\text{Trace Term}}

The data fit term penalizes the data lying outside the covariance ellipse, the complexity penalty is the integral of the data fit term over all possible observations \mathbf{y} which characterizes the volume of possible datasets, the trace term ensures the objective function is a true lower bound to the MLE of the full GP. Now, below is a table that shows the differences between each of the methods.

Algorithm \mathbf{G} \mathbf{T}
FITC diag (\mathbf{K}_{ff}-\mathbf{Q}_{ff}) + \sigma_n^2\mathbf{I} 0
VFE \sigma_n^2 \mathbf{I} \mathbf{K}_{ff}-\mathbf{Q}_{ff}
DTC \sigma_n^2 \mathbf{I} 0

Another thing to keep in mind is that the FITC algorithm approximates the model whereas the VFE algorithm approximates the inference step (the posterior). So here we just a have a difference in philosophy in how one should approach this problem. Many people in the Bayesian community will argue for approximating the inference but I think it's important to be pragmatic about these sorts of things.

Observations about the Sparse GPs

  • VFE
  • Overestimates noise variance
  • Improves with additional inducing inputs
  • Recovers the full GP Posterior
  • Hindered by local optima
  • FITC
  • Can severly underestimate the noise variance
  • May ignore additional inducing inputs
  • Does not recover the full GP posterior
  • Relies on Local Optima

Some parameter initialization strategies: * K-Means * Initially fixing the hyperparameters * Random Restarts

An interesting solution to find good hyperparameters for VFE:

  1. Find parameters with FITC solution
  2. Initialize GP model of VFE with FITC solutions
  3. Find parameters with VFE.

Source: * Understanding Probabilistic Sparse GP Approximations - Bauer et. al. (2017) - Paper * Efficient Reinforcement Learning using Gaussian Processes - Deisenroth (2010) - Thesis

Variational Compression

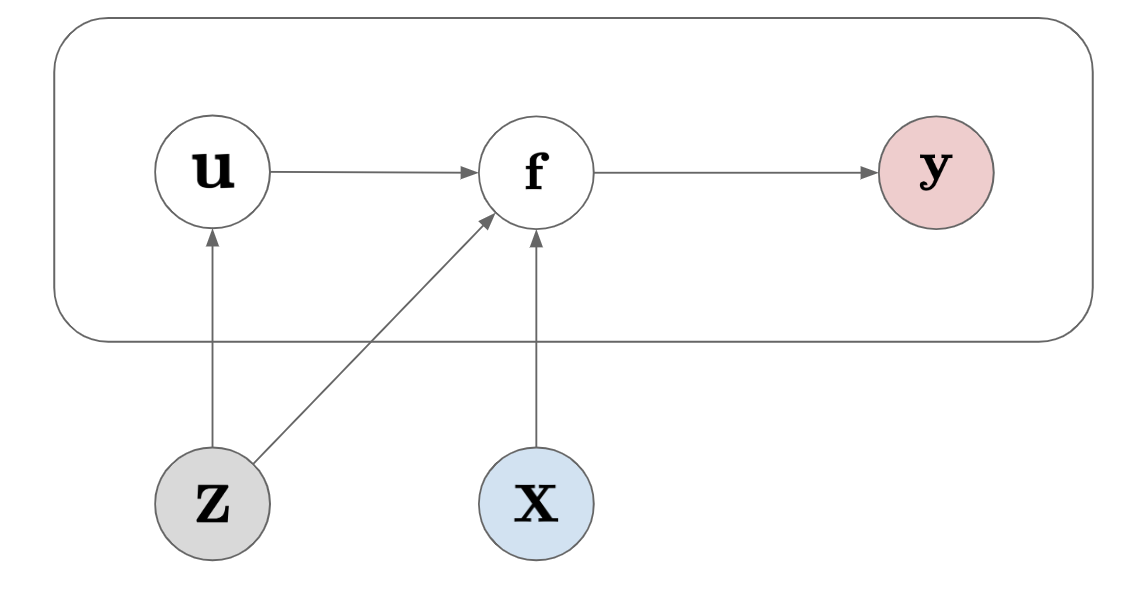
drawing

Figure: This graphical model shows the relationship between the data X, the labels y and the augmented labels z.

This is a concept I've came across that seeks to give a stronger argument for using an augmented space \mathcal Z\in \mathbb{R}^{M \times D} instead of just the data space \mathcal X \in \mathbb{R}^{N \times D}. This has allowed us to reduce the computational complexity of all of our most expensive calculations from \mathcal{O}(N^3) to \mathcal{O}(NM^2) when we are learning the best parameters for our GP models. The term variational compression comes from the notion that we want to suppress the function valuse f with some auxilary variables u. It's kind of like reducing the data space \mathcal X with the auxilary data space \mathcal Z in a principled way. This approach is very useful as it allows us to use a suite of variational inference techniques which in turn allows us to scale GP methods. In addition, we even have access to advanced optimization strategies such as stochastic variational inference and parallization strategies. You'll also notice that the GP literature has essentially formulated almost all major GP algorithm families (e.g. GP regression, GP classification and GP latent variable modeling) through this variation compression strategy. Below we will look at a nice argument; presented by Neil Lawrence (MLSS 2019); which really highlights the usefulness and cleverness of this approach and how it relates to many GP algorithms.

Joint Distribution - Augmented Space \mathcal{P}(f,u)

Let's add an additional set of variables u that's jointly Gaussian with our original function f.

p(f,u)=\mathcal{N}\left( \begin{bmatrix} f \\ u \end{bmatrix}; \begin{bmatrix} 0 \\ 0 \end{bmatrix}, \begin{bmatrix} K_{ff} & K_{fu} \\ K_{uf} & K_{uu} \end{bmatrix} \right)

We have a new space where we have introduced some auxilary variables u to be modeled jointly with f. Using all of the nice properties of Gaussian distributions, we can easily write down the conditional distribution \mathcal{P}(f|u) and marginal distribution \mathcal{P}(u) in terms of the joint distribution \mathcal P (f,u) using conditional probability rules.

\mathcal P (f,u) = \mathcal{P}(f|u) \cdot \mathcal{P}(u)

where:

  • Conditional Dist.: \mathcal{P}(\mathbf{f | u}) = \mathcal N (f| \mathbf {\mu_u, \nu^2_{uu}})
  • \mu_u = \mathbf{K_{fu}K_{uu}^{-1}u}
  • \nu^2_{uu} = \mathbf{K_{ff} - K_{fu}K_{uu}^{-1}K_{uf}}
  • Augmented space Prior: \mathcal P (\mathbf u) = \mathcal N\left( \mathbf u | 0, \mathbf K_{uu} \right)

We could actually marginalize out u to get back to the standard GP prior \mathcal P (f) = \mathcal{GP} (f | \mathbf{ m, K_{ff}}). But keep in mind that the reason why we did the conditional probability is this way is because of the computationally decreased complexity that we gain ,\mathcal{O}(N^3) \rightarrow \mathcal{O}(NM^2). We want to 'compress' the data space \mathcal X and subsequently the function space of f. So now let's write the complete joint distribution which includes the data likelihood and the augmented latent variable space:

\mathcal{P}(y,f,u|X,Z)= \underbrace{\mathcal{P}(y|f)}_{\text{Likelihood}} \cdot \underbrace{\mathcal{P} (f|u, X, Z)}_{\text{Conditional Dist.}} \cdot \underbrace{\mathcal{P}(u|Z)}_{\text{Prior}}

We have a new term which is the familiar GP likelihood term \mathcal P (y|f) = \mathcal{N}(y|f, \sigma_y^2\mathbf I). The rest of the terms we have already defined above. So now you can kind of see how we're attempting to compress the conditional distribution f. We no longer need the prior for X or f in order to obtain the joint distribution for our model. The prior we have is \mathcal P (u) which is kind of a made up variable. From henceforth, I will be omitting the dependency on X and Z as they're not important for the argument that follows. But keep it in the back of your mind that that dependency does exist.

Conditional Distribution - \mathcal{P}(y|u)

The next step would be to try and condition on f and u to obtain the conditional distribution of y given u, \mathcal{P}(y|u). We can rearrange the terms of the formula above like so:

\frac{\mathcal{P}(y,f,u)}{\mathcal{P}(u)}= \mathcal{P}(y|f) \cdot\mathcal{P}(f|u)

and using the conditional probability rules P(A,B)=P(A|B) \cdot P(B) \rightarrow P(A|B)=\frac{P(A,B)}{P(B)} we can simplify the formula even further:

\mathcal{P}(y,f|u)=\mathcal{P}(y|f) \cdot \mathcal{P}(f|u)

So, what are we looking at? We are looking at the new joint distribution of y and f given the augmented variable space that we have defined. One step closer to the conditional density. In the nature of GP models and Bayesian inference in general, the next step is to see how we obtain the marginal likelihood where we marginalize out the f's. In doing so, we obtain the conditional density that we set off to explore:

\mathcal{P}(y|u)=\int_f \mathcal{P}(y|f) \cdot \mathcal{P}(f|u) \cdot df

where: * \mathcal{P}(y|f) - Likelihood * \mathcal{P}(f|u) - Conditional Distribution

The last step would be to try and see if we can calculate \mathcal{P}(y) because if we can get a distribution there, then we can actually train our model using marginal likelihood. Unfortunately we are going to see a problem with this line of thinking when we try to do it directly. If I marginalize out the u's I get after grouping the terms:

\mathcal{P}(y)=\int_u \underbrace{\left[\int_f \mathcal{P}(y|f) \cdot \mathcal{P}(f|u) \cdot df \right]}_{\mathcal{P}(y|u)} \cdot \mathcal P(u) \cdot du

which reduces to:

\mathcal{P}(y)=\int_u \mathcal{P}(y|u) \cdot \mathcal P(u) \cdot du

This looks very similar to the parameter form of the marginal likelihood. And technically speaking this would allow us to make predictions by conditioning on the trained data \mathcal P (y*|y). The two important issues are highlighted in that equation alone:

  1. We now have the same bottleneck on our parameter for u as we do for standard Bayesian parametric modeling.
  2. The computation of \mathcal P (y|u) is not trivial calculation and we do not get any computational complexity gains trying to do that integral with the prior \mathcal P (u).

Variational Bound on \mathcal P (y|u)

We've shown the difficulties of actually obtaining the probability density function of \mathcal{P}(y) but in this section we're just going to show that we can obtain a lower bound for the conditional density function \mathcal{P}(y|u)

\mathcal{P}(y|u)=\int_f \mathcal P (y|f) \cdot \mathcal{P}(f|u) \cdot df

I'll do the 4.5 classic steps in order to arrive at a variational lower bound:

  1. Given an integral problem, take the \log of both sides of the function.
\log \mathcal P (y|u) = \log \int_f \mathcal P (y|f) \cdot \mathcal{P}(f|u) \cdot df
  1. Introduce the variational parameter q(f) as a proposal with the Identity trick.
\log \mathcal P (y|u) = \log \int_f \mathcal P (y|f) \cdot \mathcal{P}(f|u) \cdot \frac{q(f)}{q(f)} \cdot df
  1. Use Jensen's inequality for the log function to rearrange the formula to highlight the importance weight and provide a bound for \mathcal{F}(q):
\mathcal L () = \log \mathcal P (y|u) \geq \int_f q(f) \cdot \log \frac{\mathcal P (y|f) \cdot \mathcal{P}(f|u)}{q(f) } \cdot df = \mathcal F (q)
  1. Rearrange to look like an expectation and KL divergence using targeted \log rules:
\mathcal F (q) = \int_f q(f) \cdot \log \mathcal P(y|f) \cdot df - \int_f q(f) \cdot \log \frac{\mathcal{P}(f|u)}{q(f)} \cdot df
  1. Simplify notation to look like every paper in ML that uses VI to profit and obtain the variational lower bound.
\mathcal F (q) = \mathbb E_{q(f)} \left[ \log \mathcal P(y|f) \right] - \text{D}_{\text{KL}} \left[ q(f) || \mathcal{P}(f|u)\right]

Titsias Innovation: et q(f) = \mathcal{P}(f|u).

According to Titsias et al. (2009) he looked at what happens if we let q(f)=\mathcal P (f|u). For starters, without our criteria, the KL divergence went to zero and the integral we achieved will have one term less.

\log \mathcal P (y|u) \geq \int_f \mathcal P (f|u) \cdot \log \mathcal P(y|f) \cdot df

As a thought experiment though, what would happen if we had thee true posterior of \mathcal{P}(f|y,u) and an approximating density of \mathcal{P}(f|u)? Well, we can take the KL divergence of that quantity and we get the following:

\text{D}_{\text{KL}} \left[ q(f) || \mathcal{P}(f|y, u)\right] = \int_u \mathcal P (f|u) \cdot \log \frac{\mathcal P (f|u)}{\mathcal P (f|y,u)} \cdot du

According to Neil Lawrence, maximizing the lower bound minimizes the KL divergence between \mathcal{P}(f|u) and \mathcal{P}(f|u). Maximizing the bound will try to find the optimal compression and looks at the information between y and u. He does not that there is no bound and it is an exact bound when u=f. I believe that's related to the GPFlow derivation of variational GPs implementation but I don't have more information on this.

Sources:

ELBOs

Let \mathbf \Sigma = K_{ff} - K_{fu}K_{uu}^{-1}K_{fu}^{\top}

Lower Bound

\mathcal{F}= \log \mathcal{N} \left(y|0, \tilde{\mathbf K}_{ff} + \sigma_y^2\mathbf I \right) - \frac{1}{2\sigma_y^2}\text{tr}\left( \mathbf \Sigma\right)

where:

  • \tilde{\mathbf K}_{ff} = \mathbf{K_{fu}K_{uu}^{-1}K_{fu}^{\top}}
  • Nystrom approximation
  • \mathbf \Sigma = \mathbf K_{ff} - \tilde{\mathbf K}_{ff}
  • Uncertainty Based Correction

Variational Bound on \mathcal P (y)

In this scenario, we marginalize out the remaining u's and we can get an error bound on the \mathcal P(y)

\mathcal P (y) = \int_u \mathcal P (y|u) \cdot \mathcal P (u|Z) du

Source: * Nested Variational Compression in Deep Gaussian Processes - Hensman et. al. (2014) * James Hensman - GPSS 2015 | Aweseome Graphical Models

The explicit form of the lower bound \mathcal{P}(y) for is gives us:

\log \mathcal P (y) \geq \log \mathcal{N} (y|\mathbf{y|K_{fu}^{-1}m, \sigma_y^2I}) - \frac{1}{2\sigma_y^2} \text{tr}\left( \right)

Source: * Nested Variational Compression in Deep Gaussian Processes - Hensman et. al. (2014)

Stochastic Variational Inference

Supplementary Material

Important Formulas

These formulas come up when we're looking for clever ways to deal with sparse matrices in GPs. Typically we will have some matrix \mathbf K\in \mathbb R^{N\times N} which implies we need to calculate the inverse \mathbf K^{-1} and the determinant |det \mathbf K| which both require \mathcal{O}(N^3). These formulas below are useful when we want to avoid those computational complexity counts.

Nystrom Approximation

\mathbf K_{NN} \approx \mathbf U_{NM} \mathbf \Lambda_{MM} \mathbf U_{NM}^{\top}

Sherman-Morrison-Woodbury Formula

(\mathbf K_{NN} + \sigma_y^2 \mathbf I_N)^{-1} \approx \sigma_y^{-2}\mathbf I_N + \sigma_y^{-2} \mathbf U_{NM}\left( \sigma_y^{-2}\mathbf \Lambda_{MM}^{-1} + \mathbf U_{NM}^{\top} \mathbf U_{NM} \right)^{-1}\mathbf U_{NM}^{\top}

Sylvester Determinant Theorem

\left|\mathbf K_{NN} + \sigma_y^2 \mathbf I_N \right| \approx |\mathbf \Lambda_{MM} | \left|\sigma_y^{2} \mathbf \Lambda_{MM}^{-1} + U_{NM}^{\top} \mathbf U_{NM} \right|

Resources

Code Walk-Throughs

Math Walkthroughs

Papers

A good paper which highlights some import differences between the FITC, DTC and VFE. It provides a clear notational differences and also mentions how VFE is a special case of DTC. * A Unifying Framework for Gaussian Process Pseudo-Point Approximations using Power Expectation Propagation - Bui (2017)

A good summary of all of the methods under one unified framework called the Power Expectation Propagation formula.

Thesis Explain

Often times the papers that people publish in conferences in Journals don't have enough information in them. Sometimes it's really difficult to go through some of the mathematics that people put in their articles especially with cryptic explanations like "it's easy to show that..." or "trivially it can be shown that...". For most of us it's not easy nor is it trivial. So I've included a few thesis that help to explain some of the finer details. I've arranged them in order starting from the easiest to the most difficult.

Presentations

Notes

Blogs