Background - Research Notebook

Probability Density Function¶

The probability that a variate, $Y$ , has the value $y$ .

Pr[Y=y] := f(y)

(1)

Cumulative Distribution Function¶

The probability that a variate, $Y$ , takes a value less than or equal to $y$ .

Pr[Y \leq y] := F(y)

(2)

From a TPP perspective, this is known as the lifetime distribution.

F(t) = Pr[T\leq t] = 1 - S(t)

(3)

Survival Function¶

The probability that a variate, $Y$ , takes a value greater than $y$ . In other words, this gives the probability that an event will happen past a value $y$ , e.g., time.

Pr[Y > y] = 1 - Pr[Y \leq y] = 1 - F(y) := S(y)

(4)

From a TPP perspective, i.e., $S(t)$ where $t\in[0,\infty)$ , we have the following properties:

The survival function is non-increasing.
At $t=0$ , $S(t)=1$ , i.e., the probability of surviving past time 0 is 1.
At $t=\infty$ , $S(t=\infty)=0$ , i.e., as time goes to infinity, the survival curve goes to 0.

In theory, the survival function is smooth. However, in practice, we may observe events on a discrete scale. For example, on a time scale we may have days, weeks, or months.

Quantile Function¶

y_p = Pr[Y\leq y]

(5)

We can write this as the quantile function

y = F^{-1}(y_p):= Q(y_p)

(6)

We often use this function to calculate the frequency estimation like the AEP or the ARI.

Inverse Survival Function¶

This is the same as the quantile function given in equation (6) except we set the probability equal to the survival probability

y_p = 1 - y_s

(7)

Annual Exceedence Probability¶

The recurrence interval is a measure of how often an event is expected to occur based on the probability of exceeding a given stage streshold. This threshold is called the annual exceedance probability. To calculate this, we can express the return period (in years) as

R_a = R_a(T_a) = \frac{1}{T_a}

(8)

where $R_a$ is the annual exceedence probability (AEP) and $T_a$ is the number of years Wang & Holmes, 2020. The AEP is has a domain between 0 and 1, $R_a\in[0,1]$ , and the return period, $T_a$ , has a domain between 1 and infinity, $T_a\in[1,\infty)$ . This can be limiting when we consider sub-annual probabilities which would be elements less than 1. In addition, it can be incorrect when there is some wrong interpolation between 100 and 1.

A figure showing the return period [years] vs the probability of exceedance, R_a. — Figure 1:A figure showing the return period `[years]` vs the probability of exceedance, $R_a$ .

Derivation¶

This section is based off of Wang & Holmes, 2020Davison & Smith, 1990. Let $Y_t$ be an indicator variable that indicates whether in $(t,t+1]$ , at least one event occurs or not

Y_t = \begin{cases} 1, && && \text{when }N_{t+1}-N_t >0 \\ 0, && && \text{otherwise} \end{cases}

(9)

Then, $Y_t$ is a Bernoulli distribution with the probabilities

F(t) = Pr[T\leq t] = 1 - S(t)

(10)

Usage¶

In practice, we can use this to calculate the return level given any arbitrary CDF function

R_a = Pr[Y > y] = 1 - Pr[Y \leq y] = 1 - F(y; \boldsymbol{\theta})

(11)

Once we solve this for the quantity $y$ in terms of $R_p$ .

\frac{1}{T_a} = 1 - \boldsymbol{F}(y;\boldsymbol{\theta})

(12)

After we simplify the expression, we get the following relationship

y = \boldsymbol{F}^{-1}(y_p;\boldsymbol{\theta}) = \boldsymbol{Q}(y_p;\boldsymbol{\theta})

(13)

where $Q$ is the quantile function, i.e., the inverse CDF function, and $y_p = 1 - R_a = 1 - 1/T_a$ .

Average Recurrence Interval¶

The average recurrence interval (ARI) is the average time between events for a specified duration at a given location. This term is associated with partial duration series (PDS) or peak-over-thresholds (POTs). This is also known as the Mean Inter-Arrival Time or the Mean Recurrence Interval.

R_p = R_p(T_p) = 1 - \exp\left(- \frac{1}{T_p}\right)

(14)

where $T_p$ is the mean inter-arrival time measured in $years$ Wang & Holmes, 2020.

A figure showing the average recurrence interval [years] vs the probability of recurrence, R_p. — Figure 1:A figure showing the average recurrence interval `[years]` vs the probability of recurrence, $R_p$ .

Derivation¶

This section is based off of Wang & Holmes, 2020. We assume that we have a counting process, $N(A)$ , which is a Poisson process with a rate of occurrence, λ. Then the probability that there is at least 1 event in the time interval, $(0,T]$ , is given as the survival function of the exponential distribution:

Pr[N(A) \geq 1] = 1 - Pr[N(A)=0] = 1 - \exp \left(-\lambda\right)

(15)

The mean inter-arrival time is given as

\mathbb{E}[Y] = \frac{1}{\lambda} := \bar{T}, \hspace{10mm} \bar{T}\in[0,\infty)

(16)

The probability of at least 1 event in the interval $(0,T]$ is given as

Pr[N(A) \geq 1] = 1 - \exp \left(-T/ \bar{T}\right)

(17)

and the probability that there is at least 1 event within 1 unit time interval is given as

Pr[N(A) \geq 1] = 1 - \exp \left(-1/ \bar{T}\right)

(18)

Note: we can extend this for distributions where we have multiple criteria. For example, in marked HPP, we could have a 2D Poisson process given over the domain

\lambda(t,y) = \lambda f(y;\theta)

(19)

So essentially, we state that

Pr[Y>y|Y> y_0]Pr[Y>y_0] = \lambda \left(1 - F(y;\boldsymbol{\theta})\right)

(20)

So, the probability of no exceedances of $y$ over a 1-year period is given by the Poisson distribution

F_a(y) = \exp\left[ -\lambda S(y)\right]

(21)

Usage¶

In practice, we can use this to calculate the return level given any arbitrary CDF function

R_T = Pr[Y > y] = 1 - Pr[Y \leq y] = 1 - F(y;\boldsymbol{\theta})

(22)

Once we solve this for the quantity $y$ in terms of $R_T$ , we get the following relationship

y_T = \boldsymbol{Q}(y_p;\boldsymbol{\theta})

(23)

where $Q$ is the quantile function, i.e., the inverse CDF function, and $y_p = 1 - R_T = \exp\left(-1/T_p\right)$ .

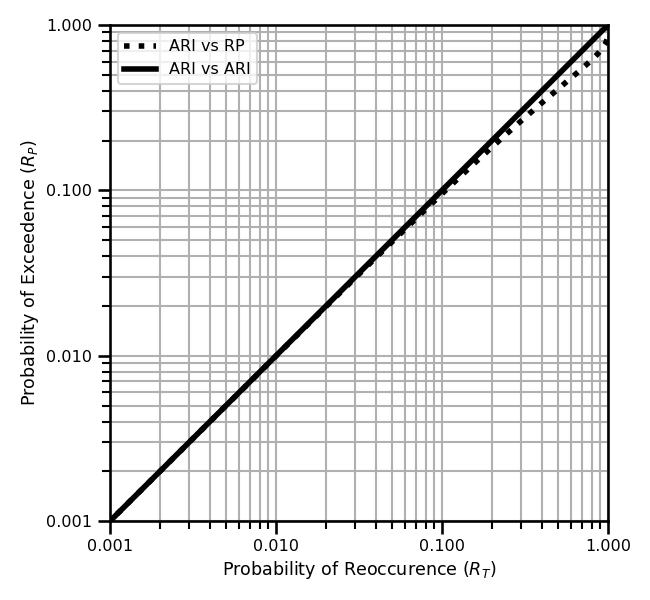
AEP vs ARI¶

There are some equivalences of these two quantities. Namely, we can write this as:

\begin{aligned} R_p &= R_a \\ \frac{1}{T_a} &= 1 - \exp\left(- \frac{1}{T_p}\right) \end{aligned}

(24)

Figure 3 showcases the AEP vs the probability of recurrence. We see that they are almost the same except for near the upper tail. Figure 4 demonstrates the relationship better. We see that the ARI has the domain between $T_p \in [0, \infty)$ whereas the RP has the domain between $R_p \in [0, \infty)$ . So, there is a relationship between the two quantities but they are not the same due to the differences in the domain.

Probabilities

Periods

A figure showing the probability of occurrence, R_a, vs the probability of exceedence, R_p. — Figure 3:A figure showing the probability of occurrence, $R_a$ , vs the probability of exceedence, $R_p$ .

Hazard Function¶

The ratio of probability density function to the survival function, aka the conditional failure density function.

H(y) = \int_{-\infty}^yh(\tau)d\tau = -\log\left(1-F(y)\right)=- \log S(y)

(25)

Counting Process¶

\begin{aligned} N(A) &= \#\left\{n\in\mathbb{N}^+: T_n \in A \right\} \\ &= \sum_{n=1}^\infty \mathcal{1} (T_n \in A) \end{aligned}

(26)

Survival Function¶

This is the probability that the time of death is later than some specified time, $t$ .

S(t) = Pr[T>t] = \int_t^\infty f(\tau)d\tau = 1 - F(t)

(27)

Event Density¶

This is the rate of death/failure events per unit time

f(t) = F'(t) = \frac{d}{dt}F(t)

(28)

Survival Event Density¶

\begin{aligned} s(t) &= S'(t) = \frac{d}{dt}S(t) \\ &= \frac{d}{dt}\int_t^\infty f(\tau)d\tau \\ &= \frac{d}{dt}\left[1 - F(t) \right] \\ &= - f(t) \end{aligned}

(29)

Conditional Intensity Function¶

This is the instantaneous rate of a new arrival of new events at time, $t$ , given a history of past events, $\mathcal{H}_t$ . This is also known as the hazard function.

\lambda^*(t) = \frac{f^*(t)}{1-F^*(t)}

(30)

We can rewrite this using th relationship of the survival function

\lambda^*(t) = \frac{f^*(t)}{S^*(t)}

(31)

We can also rewrite this using the relationship between the survival function and the cumulative hazard function

\lambda^*(t) = \frac{f^*(t)}{\exp\left( -\Lambda(\mathcal{T}) \right)}

(32)

Cumulative Hazard Function¶

In general, there are four properties it needs to satisfy

\begin{aligned} \Lambda^*(t) &> 0 \\ \Lambda^*(t_n) &= 0 \\ \lim_{t\rightarrow \infty} \Lambda^*(t) &= \infty \\ \frac{d \Lambda^*(t)}{dt} &> 0 \end{aligned}

(33)

This is achieved by always having a positive outcome within hazard function parameterization.

Probability Density Function¶

We can write the conditional probability density function in terms of the hazard and cumulative hazard function

f^*(t) = \lambda^*(t) \exp\left( -\Lambda(T) \right) = \lambda^*(t)S^*(t)

(34)

We can also write it using the hazard function and the survival function

f^*(t) = \lambda^*(t)S^*(t)

(35)

And lastly, we can write it in terms of the hazard function and the CDF function.

f^*(t) = \lambda^*(t)\left(1-F^*(t)\right)

(36)

References¶

Wang, C.-H., & Holmes, J. D. (2020). Exceedance rate, exceedance probability, and the duality of GEV and GPD for extreme hazard analysis. Natural Hazards, 102(3), 1305–1321. 10.1007/s11069-020-03968-z
Davison, A. C., & Smith, R. L. (1990). Models for Exceedances Over High Thresholds. Journal of the Royal Statistical Society Series B: Statistical Methodology, 52(3), 393–425. 10.1111/j.2517-6161.1990.tb01796.x