Modern 4DVar

State Estimation - Weak Constrained 4DVar

How to estimate the state using a dynamical ODE

CNRS
MEOM 
import os, sys

jaxsw_path = "/Users/eman/code_projects/jaxsw"
sys.path.append(jaxsw_path)
import autoroot  # noqa: F401, I001
import jax
import jax.numpy as jnp
import jax.random as jrandom
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import diffrax as dfx
import equinox as eqx
import xarray as xr
import functools as ft

from jaxsw import L63State, Lorenz63, rhs_lorenz_63

jax.config.update("jax_enable_x64", True)

sns.reset_defaults()
sns.set_context(context="talk", font_scale=0.7)

%matplotlib inline
%load_ext autoreload
%autoreload 2
The autoreload extension is already loaded. To reload it, use:
  %reload_ext autoreload

Lorenz 63

  • Equation of Motion
  • Observation Operator
  • Integrate

Equation of Motion

dxdt=σ(y−x)dydt=x(ρ−z)−ydzdt=xy−βz\begin{aligned} \frac{dx}{dt} &= \sigma (y - x) \\ \frac{dy}{dt} &= x (\rho - z) - y \\ \frac{dz}{dt} &= xy - \beta z \end{aligned}
(1)

where (σ,ρ,β)(\sigma,\rho,\beta) are hyperparameters.

Simulation

ds_sol = xr.open_dataset("./data/sim_l63.nc")
ds_sol
Loading...

Inverse Problem

realization = 100

ds_trajectory = ds_sol.sel(realization=realization)
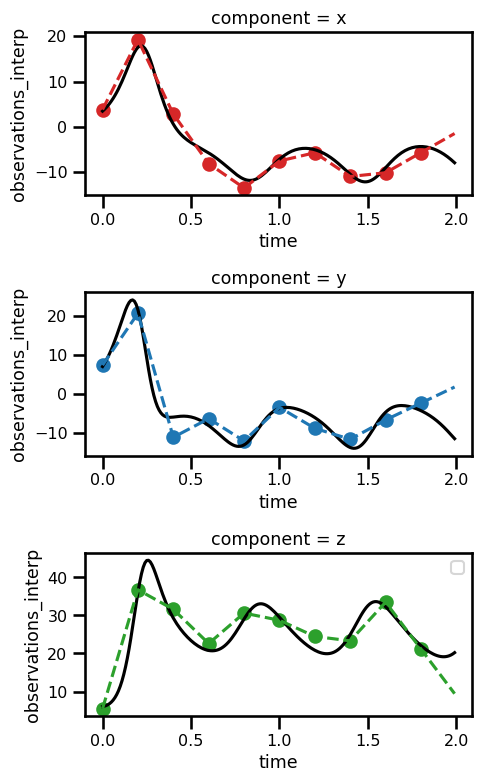
ds_trajectory
Loading...
fig, ax = plt.subplots(nrows=3, figsize=(5, 8))


ds_trajectory.simulation.sel(component="x").plot(ax=ax[0], color="black")
ds_trajectory.simulation.sel(component="y").plot(ax=ax[1], color="black")
ds_trajectory.simulation.sel(component="z").plot(ax=ax[2], color="black")

ds_trajectory.observations_noise.sel(component="x").plot.scatter(
    ax=ax[0], color="tab:red"
)
ds_trajectory.observations_noise.sel(component="y").plot.scatter(
    ax=ax[1], color="tab:blue"
)
ds_trajectory.observations_noise.sel(component="z").plot.scatter(
    ax=ax[2], color="tab:green"
)

ds_trajectory.observations_interp.sel(component="x").plot(
    ax=ax[0], color="tab:red", linestyle="--"
)
ds_trajectory.observations_interp.sel(component="y").plot(
    ax=ax[1], color="tab:blue", linestyle="--"
)
ds_trajectory.observations_interp.sel(component="z").plot(
    ax=ax[2], color="tab:green", linestyle="--"
)

# ax.set_xlabel("Time")
# ax.set_ylabel("Values")
# ax.set_title(f"Trajectory")


plt.legend()
plt.tight_layout()
plt.show()
No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
<Figure size 500x800 with 3 Axes>

Data

For this problem we need the following variables

True State: u\boldsymbol{u}

Time Steps: T\boldsymbol{\Tau}

Observations: y\boldsymbol{y}

Initial State: u(k)\boldsymbol{u}^{(k)}

Mask: m\boldsymbol{m}

# Ground Truth
x_state = jnp.asarray(ds_trajectory.simulation.values).T.astype(jnp.float64)
ts_state = jnp.asarray(ds_trajectory.time.values).astype(jnp.float64)
# Observations
y_gt = jnp.asarray(ds_trajectory.observations_noise.values).T.astype(jnp.float64)
# Mask
y_mask = 1.0 - (
    jnp.isnan(jnp.asarray(ds_trajectory.observations_noise.values))
    .astype(jnp.float32)
    .T.astype(jnp.float64)
)
# initialization
x_init = jnp.asarray(ds_trajectory.observations_interp.values).T.astype(jnp.float64)

x_state.shape, y_gt.shape, y_mask.shape, x_init.shape
((200, 3), (200, 3), (200, 3), (200, 3))

Dynamical Prior

Here, we define our dynamical prior which we plug into this loss function.

R(u;θ)=λ2∣∣u−ϕ(u;θ)∣∣22\mathbf{R}(\boldsymbol{u};\boldsymbol{\theta}) = \frac{\lambda}{2} ||\boldsymbol{u} - \boldsymbol{\phi}(\boldsymbol{u};\boldsymbol{\theta})||_2^2
(2)

Our dynamical prior in this case is defined by:

ϕ(u;θ)≔u(t1)=u(t0)+∫t0t1F(u(t),τ;θ)dτ\boldsymbol{\phi}(\boldsymbol{u};\boldsymbol{\theta}) \coloneqq \boldsymbol{u}(t_1) = \boldsymbol{u}(t_0) + \int_{t_0}^{t_1} \boldsymbol{F}\left( \boldsymbol{u}(t),\tau;\boldsymbol{\theta}\right)d\tau
(3)

Weak Constrained

The weak-constrained version works as a "one-step" prediction whereby we step through the trajectory with the ODE solver one at a time.

R(u;θ)=λ2∑t=0T∣∣ut−ϕ(ut;θ)∣∣22\mathbf{R}(\boldsymbol{u};\boldsymbol{\theta}) = \frac{\lambda}{2} \sum_{t=0}^T ||\boldsymbol{u}_t - \boldsymbol{\phi}(\boldsymbol{u}_t;\boldsymbol{\theta})||_2^2
(4)
from mfourdvar._src.priors.dynamical import DynIncrements, DynTrajectory
from jaxsw import L63State, L63Params
import typing as tp
from jaxtyping import Array, PyTree

class L63Params(eqx.Module):
    sigma: Array = eqx.static_field()
    rho: Array = eqx.static_field()
    beta: Array = eqx.static_field()
    
    def __init__(self, sigma: float=10., rho: float=28., beta: float=2.667):
        self.sigma = jnp.asarray(sigma, dtype=jnp.float64)
        self.rho = jnp.asarray(rho, dtype=jnp.float64)
        self.beta = jnp.asarray(beta, dtype=jnp.float64)

class L63Model(eqx.Module):
    model: PyTree

    def init_state(self, x: PyTree) -> PyTree:
        state = L63State(
            x=jnp.atleast_1d(x[..., 0]), 
            y=jnp.atleast_1d(x[..., 1]), 
            z=jnp.atleast_1d(x[..., 2])
        )
        return state
    
    def __call__(self, t, state, args):
        return self.model.equation_of_motion(t, state, args)
# init dynamical system
l63_dyn_model = Lorenz63()

# initialize prior model
prior_model = L63Model(model=l63_dyn_model)


# initialize state
state_init = prior_model.init_state(x_init)

# initialize params
params = L63Params(sigma=10., rho=28., beta=2.667)


# output state
state_out = prior_model(0, state_init, params)

# check input and output are the same
assert state_init.x.shape == state_out.x.shape
assert state_init.y.shape == state_out.y.shape
assert state_init.z.shape == state_out.z.shape
# initialize dynamical prior
prior = DynIncrements(model=prior_model, params=params)
from mfourdvar._src.utils import time_patches
ts_patches = time_patches(ts_state)
out = jax.vmap(prior, in_axes=(0,0), out_axes=(0))(x_init[:-1], ts_patches)
out.array.shape, out.y.shape
((199, 3), (199, 1, 1))

Sanity Check

In this sanity check, we're going to compare two losses: a) one set of inputs will be the true state propagated through the 1 step ODE model and b) one loss of inputs will be the state initialized via the naive interpolation scheme.

In prinicpal, the absolute loss value should be more for the state initialized with the naive interpolation.

loss_true = prior.loss(x=x_state, ts=ts_state)

loss_init = prior.loss(x=x_init, ts=ts_state)

loss_init_state = prior.loss(x=x_init, ts=ts_state, x_gt=x_state)

# check hypothesis
assertion = loss_init > loss_true

msg = f"Loss\n----"
msg = f""
msg += f"\nInit+True State: {loss_init:.2f}"
print(
    f"Loss\n----"+
    f"\nTrue State: {loss_true:.2f}" +
    f"\nInit State: {loss_init:.2f}" +
    f"\nInit+True State: {loss_init_state:.2f}" +
    f"\nLess: {assertion}"
)
Loss
----
True State: 0.00
Init State: 137.11
Init+True State: 6027.93
Less: True

We see that this is the case!

Note: The loss is not exactly zero as one might initially suspect. However, this may be the case because we are stepping iteratively one-step at a time instead of simply predicting using the full trajectory. This may have some accumulated error somewhere in these many steps.

Learning

In this instance, we're going to use a simple gradient descent scheme.

u(k+1)=u(k)+α∇uJ(u;θ)\boldsymbol{u}^{(k+1)} = \boldsymbol{u}^{(k)} + \alpha \boldsymbol{\nabla_u}\boldsymbol{J}(\boldsymbol{u};\boldsymbol{\theta})
(5)

where α\alpha is the learning rate and ∇u\boldsymbol{\nabla_u} is the gradient operator wrt the state, u\boldsymbol{u}. We have an optimality condition of the gradient of the variational cost.

Fg(u;θ)=∇uJ(u;θ)\boldsymbol{F_g}(\boldsymbol{u};\boldsymbol{\theta}) = \boldsymbol{\nabla_u}\boldsymbol{J}(\boldsymbol{u};\boldsymbol{\theta})
(6)

Because we are doing gradient descent, we will use a negative learning rate of α=−0.1\alpha=-0.1.

For this first part, we're simply going to use the variational cost as the dynamical prior.

J(u;θ)=R(u;θ)=λ2∑t=0T∣∣ut−ϕ(ut;θ)∣∣22\begin{aligned} \boldsymbol{J}(\boldsymbol{u};\boldsymbol{\theta}) &= \boldsymbol{R}(\boldsymbol{u};\boldsymbol{\theta}) \\ &= \frac{\lambda}{2} \sum_{t=0}^T ||\boldsymbol{u}_t - \boldsymbol{\phi}(\boldsymbol{u}_t;\boldsymbol{\theta})||_2^2 \end{aligned}
(7)
# create grad loss function
grad_loss_fn = jax.jit(jax.value_and_grad(prior.loss, has_aux=False))
from tqdm.autonotebook import trange

losses = []
num_iterations = 30_000
learning_rate = - 0.2
x = x_init.copy()
# # x_gt = x_init
# x_gt = x_state.copy()

# loop through learning
with trange(num_iterations) as pbar:
    for i in pbar:

        # get dynamical loss + gradient
        loss, x_grad = grad_loss_fn(x, ts_state)

        pbar.set_description(f"Loss: {loss:.2e}")
        losses.append(loss)

        # clip gradients
        x_grad = jnp.clip(x_grad, a_min=-1.0, a_max=1.0)

        # update solution with gradient
        x += learning_rate * x_grad
Loading...
fig, ax = plt.subplots()

ax.plot(losses)

ax.set(
    yscale="log", 
    xscale="log",
    xlabel="Iterations", 
    ylabel="Prior Loss"
)
plt.show()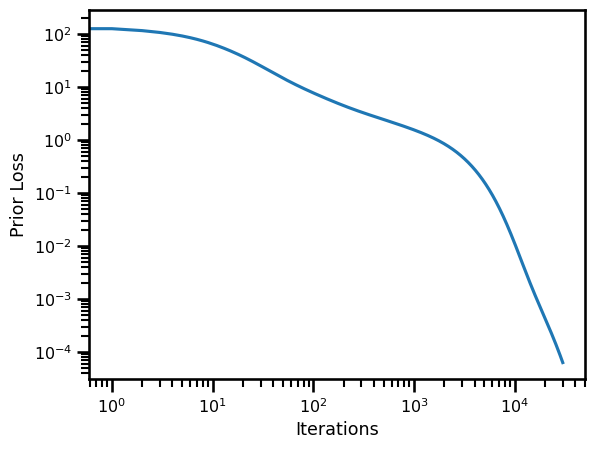
<Figure size 640x480 with 1 Axes>
ds_results = xr.Dataset(
    {
        "x": (("time"), x[:, 0].squeeze()),
        "y": (("time"), x[:, 1].squeeze()),
        "z": (("time"), x[:, 2].squeeze()),
    },
    coords={
        "time": (["time"], ts_state.squeeze()),
    },
    attrs={
        "ode": "lorenz_63",
        "sigma": params.sigma,
        "beta": params.beta,
        "rho": params.rho,
    },
)

ds_results = ds_results.to_array(dim="component", name="prediction").to_dataset()
ds_results["state"] = (
    (
        "component",
        "time",
    ),
    x_state.T,
)
ds_results["initialization"] = (
    (
        "component",
        "time",
    ),
    x_init.T,
)
ds_results["observation"] = (
    (
        "component",
        "time",
    ),
    y_gt.T,
)
# ds_results.x_state
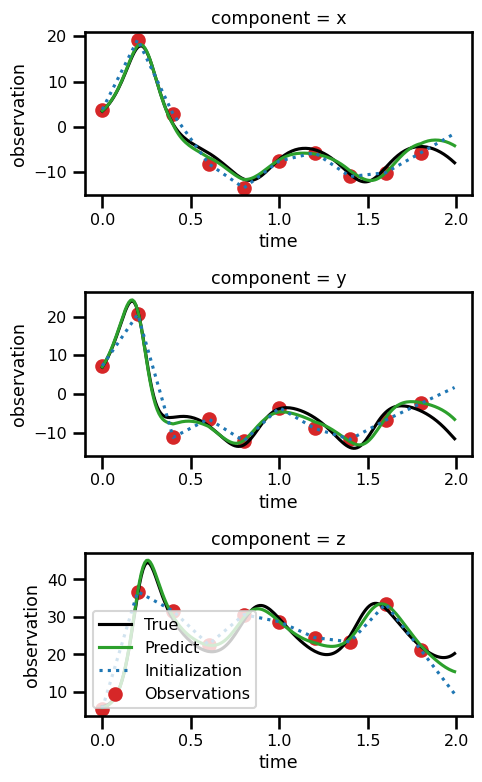
ds_results
Loading...
fig, ax = plt.subplots(nrows=3, figsize=(5, 8))

for axis in range(3):
    ds_results.state.isel(component=axis).plot(
        ax=ax[axis], linestyle="-", color="black", label="True"
    )
    ds_results.prediction.isel(component=axis).plot(
        ax=ax[axis], linestyle="-", color="tab:green", label="Predict"
    )
    ds_results.initialization.isel(component=axis).plot(
        ax=ax[axis], linestyle=":", color="tab:blue", label="Initialization"
    )
    ds_results.observation.isel(component=axis).plot.scatter(
        ax=ax[axis], color="tab:red", label="Observations"
    )
    plt.legend()


# plt.legend()
plt.tight_layout()
plt.show()
No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
<Figure size 500x800 with 3 Axes>

Observation Operator

L(u;θ)=λobs∣∣y−H(u;θ)∣∣22\boldsymbol{L}(\boldsymbol{u};\boldsymbol{\theta}) = \lambda_{obs}|| \boldsymbol{y} - \boldsymbol{H}(\boldsymbol{u};\boldsymbol{\theta})||_2^2
(8)

We can use a simpler loss function which is just a masking operator.

L(u;θ)=λobs∣∣y−u∣∣Ωobs2\boldsymbol{L}(\boldsymbol{u};\boldsymbol{\theta}) = \lambda_{obs}|| \boldsymbol{y} - \boldsymbol{u}||_{\Omega_{obs}}^2
(9)

where Ωobs\Omega_{obs} is the domain of the observation.

from mfourdvar._src.operators.base import ObsOperator

obs_operator = ObsOperator()

obs_operator.loss(x_init, y_gt, y_mask)
Array(0., dtype=float64)

Variational Cost

from mfourdvar._src.varcost.dynamical import WeakVarCost
# compute initial condition
x = x_init.copy()
x_gt = x_state.copy()

# init dynamical system
l63_dyn_model = Lorenz63()

# initialize prior model
prior_model = L63Model(model=l63_dyn_model)
# initialize params
params = L63Params(sigma=10., rho=28., beta=2.667)
# initialize dynamical prior
prior = DynIncrements(model=prior_model, params=params)

# initialize observation operator
obs_operator = ObsOperator()

# initialize variational cost function
prior_weight = 0.9
obs_op_weight = 0.05
background_weight = 0.05
varcost_fn = WeakVarCost(
    prior=prior, 
    obs_op=obs_operator, 
    prior_weight=prior_weight, 
    obs_op_weight=obs_op_weight, 
    background_weight=background_weight
)


# compute variational cost
loss_init, losses_init = varcost_fn.loss(x=x_init, ts=ts_state, y=y_gt, mask=y_mask, return_loss=True)
loss_true, losses_true = varcost_fn.loss(x=x_state, ts=ts_state, y=y_gt,  x_gt=x_state, mask=y_mask, return_loss=True)
loss_init_true, losses_init_true = varcost_fn.loss(x=x_init, ts=ts_state, y=y_gt,  x_gt=x_state, mask=y_mask, return_loss=True)
print("True State vs True State")
print(losses_true)
print("Init X vs Init State") 
print(losses_init)
print("Init X vs True State")
print(losses_init_true)
True State vs True State
{'var_loss': Array(5.17501827, dtype=float64), 'prior': Array(2.11213048e-06, dtype=float64), 'obs': Array(103.50032733, dtype=float64), 'bg': Array(5.17501827, dtype=float64)}
Init X vs Init State
{'var_loss': Array(123.39489731, dtype=float64), 'prior': Array(137.10544146, dtype=float64), 'obs': Array(0., dtype=float64), 'bg': Array(123.39489731, dtype=float64)}
Init X vs True State
{'var_loss': Array(5425.14077045, dtype=float64), 'prior': Array(6027.93418939, dtype=float64), 'obs': Array(0., dtype=float64), 'bg': Array(5425.14077045, dtype=float64)}

Learning

import functools as ft


@ft.partial(jax.value_and_grad, has_aux=True)
def loss_function_state(x_init):    
    return varcost_fn.loss(x=x_init, ts=ts_state, y=y_gt, mask=y_mask, xb=x_state[0], return_loss=True)

(loss, _), grads = loss_function_state(x_init)
print(grads.shape)

@eqx.filter_value_and_grad(has_aux=True)
def loss_function_state(x_init):    
    return varcost_fn.loss(x=x_init, ts=ts_state, y=y_gt, mask=y_mask, xb=x_state[0], return_loss=True)

(loss, _), grads = loss_function_state(x_init)
print(grads.shape)
(200, 3)
(200, 3)

from tqdm.autonotebook import trange

losses = dict(prior=[], obs=[], bg=[], var_loss=[])
num_iterations = 2_000
learning_rate = - 0.2
x = x_init.copy()

# loop through learning
with trange(num_iterations) as pbar:
    for i in pbar:

        # get dynamical loss + gradient
        (_, loss), x_grad = loss_function_state(x)

        losses["var_loss"].append(loss["var_loss"])
        losses["prior"].append(loss["prior"])
        losses["obs"].append(loss["obs"])
        losses["bg"].append(loss["bg"])

        pbar_msg = f"Var Loss: {loss['var_loss']:.2e} | "
        pbar_msg += f"Prior - {loss['prior']:.2e} | "
        pbar_msg += f"Obs - {loss['obs']:.2e} | "
        pbar_msg += f"BG - {loss['bg']:.2e}"
        pbar.set_description(pbar_msg)

        # clip gradients
        x_grad = jnp.clip(x_grad, a_min=-1.0, a_max=1.0)

        # update solution with gradient
        x += learning_rate * x_grad
Loading...
# compute variational cost
loss_init, losses_init = varcost_fn.loss(x=x_init, ts=ts_state, y=y_gt, mask=y_mask, return_loss=True)
loss_true, losses_true = varcost_fn.loss(x=x_state, ts=ts_state, y=y_gt,  x_gt=x_state, mask=y_mask, return_loss=True)
loss_init_true, losses_init_true = varcost_fn.loss(x=x_init, ts=ts_state, y=y_gt,  x_gt=x_state, mask=y_mask, return_loss=True)
loss_sol_true, losses_sol_true = varcost_fn.loss(x=x, ts=ts_state, y=y_gt,  x_gt=x_state, mask=y_mask, return_loss=True)
loss_sol, losses_sol = varcost_fn.loss(x=x, ts=ts_state, y=y_gt, mask=y_mask, return_loss=True)
print("True State vs True State")
print(losses_true)
print("Init X vs Init State") 
print(losses_init)
print("Init X vs True State")
print(losses_init_true)
print("Sol State vs True State")
print(losses_sol_true)
print("Sol state")
print(losses_sol)
True State vs True State
{'var_loss': Array(5.17501827, dtype=float64), 'prior': Array(2.11213048e-06, dtype=float64), 'obs': Array(103.50032733, dtype=float64), 'bg': Array(5.17501827, dtype=float64)}
Init X vs Init State
{'var_loss': Array(123.39489731, dtype=float64), 'prior': Array(137.10544146, dtype=float64), 'obs': Array(0., dtype=float64), 'bg': Array(123.39489731, dtype=float64)}
Init X vs True State
{'var_loss': Array(5425.14077045, dtype=float64), 'prior': Array(6027.93418939, dtype=float64), 'obs': Array(0., dtype=float64), 'bg': Array(5425.14077045, dtype=float64)}
Sol State vs True State
{'var_loss': Array(906.05181181, dtype=float64), 'prior': Array(1004.14436518, dtype=float64), 'obs': Array(46.43766306, dtype=float64), 'bg': Array(906.05181181, dtype=float64)}
Sol state
{'var_loss': Array(3.37225144, dtype=float64), 'prior': Array(1.16707587, dtype=float64), 'obs': Array(46.43766306, dtype=float64), 'bg': Array(3.37225144, dtype=float64)}

fig, ax = plt.subplots()

ax.plot(losses["prior"], label="Prior", linestyle=":")
ax.plot(losses["obs"], label="Observations", linestyle=":")
ax.plot(losses["bg"], label="Background", linestyle=":")
ax.plot(losses["var_loss"], label="Variational", zorder=0)

ax.set(
    yscale="log",
    xscale="log",
    xlabel="Iterations", 
    ylabel="Loss"
)

plt.legend()
plt.show()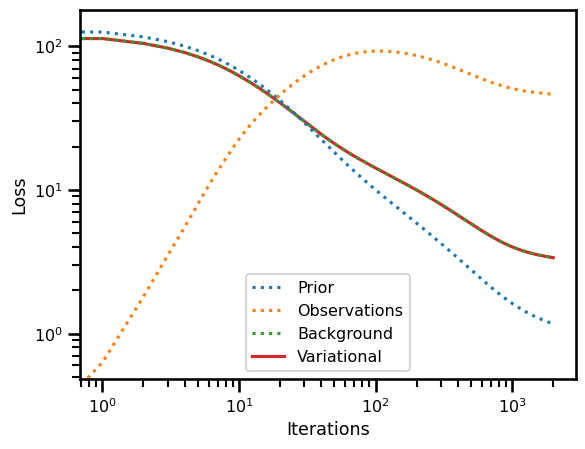
<Figure size 640x480 with 1 Axes>
ds_results = xr.Dataset(
    {
        "x": (("time"), x[:, 0].squeeze()),
        "y": (("time"), x[:, 1].squeeze()),
        "z": (("time"), x[:, 2].squeeze()),
    },
    coords={
        "time": (["time"], ts_state.squeeze()),
    },
    attrs={
        "ode": "lorenz_63",
        "sigma": params.sigma,
        "beta": params.beta,
        "rho": params.rho,
    },
)

ds_results = ds_results.to_array(dim="component", name="prediction").to_dataset()
ds_results["state"] = (
    (
        "component",
        "time",
    ),
    x_state.T,
)
ds_results["initialization"] = (
    (
        "component",
        "time",
    ),
    x_init.T,
)
ds_results["observation"] = (
    (
        "component",
        "time",
    ),
    y_gt.T,
)
# ds_results.x_state
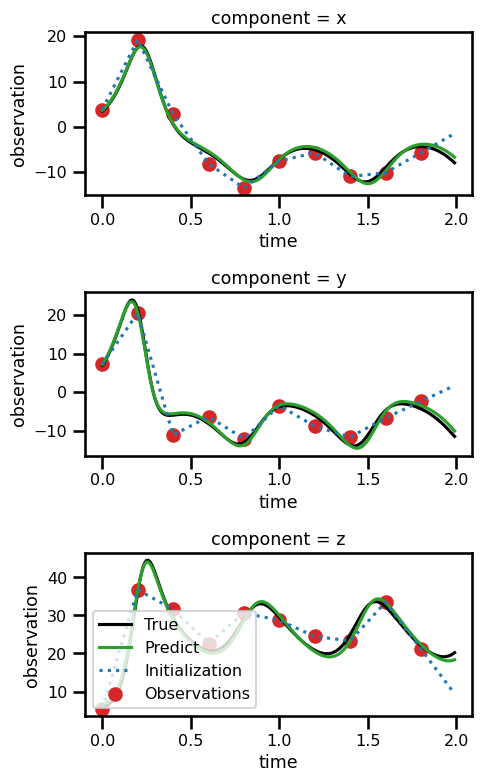
ds_results
Loading...
fig, ax = plt.subplots(nrows=3, figsize=(5, 8))

for axis in range(3):
    ds_results.state.isel(component=axis).plot(
        ax=ax[axis], linestyle="-", color="black", label="True"
    )
    ds_results.prediction.isel(component=axis).plot(
        ax=ax[axis], linestyle="-", color="tab:green", label="Predict"
    )
    ds_results.initialization.isel(component=axis).plot(
        ax=ax[axis], linestyle=":", color="tab:blue", label="Initialization"
    )
    ds_results.observation.isel(component=axis).plot.scatter(
        ax=ax[axis], color="tab:red", label="Observations"
    )
    plt.legend()


# plt.legend()
plt.tight_layout()
plt.show()
No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
<Figure size 500x800 with 3 Axes>
Example - Lorenz-63
State Est. - Strong
Resources
Code