1D Burgers Equation

J. Emmanuel JohnsonTakaya Uchida

Jax-ify
Don't Reinvent the Wheel

import autoroot
import jax
import jax.numpy as jnp
import numpy as np
import equinox as eqx
import kernex as kex
import finitediffx as fdx
import diffrax as dfx
import xarray as xr
import matplotlib.pyplot as plt
import seaborn as sns
from tqdm.notebook import tqdm, trange
from jaxtyping import Float, Array, PyTree, ArrayLike
import wandb
from jaxsw._src.domain.base import Domain
from jaxsw._src.models.pde import DynamicalSystem
from jaxsw._src.domain.time import TimeDomain

sns.reset_defaults()
sns.set_context(context="talk", font_scale=0.7)
jax.config.update("jax_enable_x64", True)

%matplotlib inline
%load_ext autoreload
%autoreload 2

Let's start with a simple 2D Linear Advection scheme. This PDE is defined as:

\begin{aligned} \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} &= \nu\frac{\partial^2 u}{\partial x^2} \end{aligned}

(1)

Here, we are advised to a backwards difference for the advection term, a second order central difference for the diffusion term and a first order time stepper for the time derivative.

Domain¶

nx = 101
xmin = 0.0
xmax = 2.0 * jnp.pi

Domain??

Init signature: Domain(*args, **kwargs)
Source:        
class Domain(eqx.Module):
    """Domain class for a rectangular domain

    Attributes:
        size (Tuple[int]): The size of the domain
        xmin: (Iterable[float]): The min bounds for the input domain
        xmax: (Iterable[float]): The max bounds for the input domain
        coord (List[Array]): The coordinates of the domain
        grid (Array): A grid of the domain
        ndim (int): The number of dimenions of the domain
        size (Tuple[int]): The size of each dimenions of the domain
        cell_volume (float): The total volume of a grid cell
    """

    xmin: tp.Iterable[float] = eqx.static_field()
    xmax: tp.Iterable[float] = eqx.static_field()
    dx: tp.Iterable[float] = eqx.static_field()

    def __init__(self, xmin, xmax, dx):
        """Initializes domain
        Args:
            xmin (Iterable[float]): the min bounds for the input domain
            xmax (Iterable[float]): the max bounds for the input domain
            dx (Iterable[float]): the step size for the input domain
        """
        assert len(xmin) == len(xmax)
        dx = _check_and_return(dx, ndim=len(xmin), name="dx")
        self.xmin = xmin
        self.xmax = xmax
        self.dx = dx

    @classmethod
    def from_numpoints(
        cls,
        xmin: tp.Iterable[float],
        xmax: tp.Iterable[float],
        N: tp.Iterable[int],
    ):
        f = lambda xmin, xmax, N: (xmax - xmin) / (float(N) - 1)

        dx = tuple(map(f, xmin, xmax, N))

        return cls(xmin=xmin, xmax=xmax, dx=dx)

    @property
    def coords(self) -> tp.List:
        return list(map(make_coords, self.xmin, self.xmax, self.dx))

    @property
    def grid(self) -> jnp.ndarray:
        return make_grid_from_coords(self.coords)

    @property
    def ndim(self) -> int:
        return len(self.xmin)

    @property
    def size(self) -> tp.Tuple[int]:
        return tuple(map(len, self.coords))

    @property
    def Nx(self) -> tp.Tuple[int]:
        return self.size

    @property
    def Lx(self) -> tp.Tuple[int]:
        f = lambda xmin, xmax: xmax - xmin
        return tuple(map(f, self.xmin, self.xmax))

    @property
    def cell_volume(self) -> float:
        return reduce(mul, self.dx)
File:           ~/code_projects/jaxsw/jaxsw/_src/domain/base.py
Type:           _ModuleMeta
Subclasses:

domain = Domain.from_numpoints(xmin=(xmin,), xmax=(xmax,), N=(nx,))

print(f"Nx: {domain.Nx}")
print(f"Lx: {domain.Lx}")
print(f"dx: {domain.dx}")
print(f"nDims: {domain.ndim}")
print(f"Grid Size: {domain.grid.shape}")
print(f"Cell Volume: {domain.cell_volume}")

Nx: (101,)
Lx: (6.283185307179586,)
dx: (0.06283185307179587,)
nDims: 1
Grid Size: (101, 1)
Cell Volume: 0.06283185307179587

Initial Conditions¶

This probably has the most complicated initialization function I've seen in a while. It contains two functions:

\begin{aligned} u(x,t,\nu) &= - \frac{2\nu}{\phi}\frac{\partial \phi}{\partial x} + 4 \\ \phi(x,t,\nu) &= \exp\left(\frac{-(x-4t)^2}{4\nu(t+1)}\right) + \exp\left(\frac{-(x-4t-2\pi)^2}{4\nu(t+1)}\right) \end{aligned}

(2)

Notice that the $\boldsymbol{u}(x,t,\nu)$ has another function $\phi$ as well as its partial derivative wrt to $x$ , $\partial_x\phi$ .

import functools as ft


def phi(x, t, nu):
    denominator = 4 * nu * (t + 1)
    t1 = jnp.exp(-((x - 4 * t) ** 2) / denominator)
    t2 = jnp.exp(-((x - 4 * t - 2 * jnp.pi) ** 2) / denominator)
    return t1 + t2

In the original tutorial, they used sympy to calculate the derivative analytically and then they created a function. I'm a bit lazy, so I will simply use autodifferentiation to calculate the gradient exactly

dphi_dx = jax.grad(phi, argnums=0)

Below, I use a nifty decorator to create a function that auto-vectorizes over the first argument.

@ft.partial(jax.vmap, in_axes=(0, None, None))
def init_u(x, t, nu):
    c = phi(x, t, nu)

    u = -((2 * nu) / c) * dphi_dx(x, t, nu) + 4

    return u

Now we can use this to initialize the Burger's function.

nu = 0.07
t = 0.0

u_init = init_u(domain.coords[0], 0, nu)

assert u_init.shape == domain.coords[0].shape

fig, ax = plt.subplots(figsize=(5, 3))

ax.plot(domain.grid.squeeze(), u_init)

plt.show()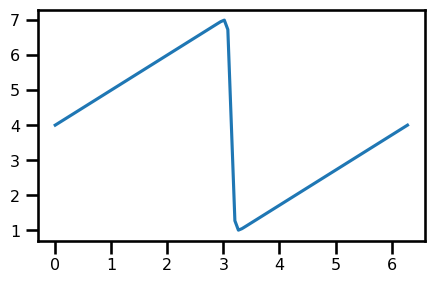

Boundary Conditions¶

For the boundary conditions, we will use periodic boundary conditions.

\mathcal{BC}[u](x, t) = ..., \hspace{10mm} x\in\partial\Omega \hspace{3mm} t\in\mathcal{T}

(3)

def bc_fn(u: Float[Array, "D"]) -> Float[Array, "D"]:
    u = u.at[0].set(u[-1])

    return u

u_out = bc_fn(u_init)

Equation of Motion¶

Looking at the previous equation (1) for Burgers 1D: Because we are doing advection, we will use backwards difference for each of the terms.

\begin{aligned} \frac{\partial u}{\partial t} + uD^-[u] &= \nu D^2[u] \end{aligned}

(4)

where $D$ is the central finite difference method.

from typing import Optional
from jaxsw._src.operators.functional import advection, diffusion


class Burgers1D(DynamicalSystem):
    @staticmethod
    def equation_of_motion(t: float, u: Array, args):
        u = bc_fn(u)

        nu, domain = args

        rhs_adv = advection.advection_1D(u=u, a=u, step_size=domain.dx)

        # rhs_adv = advection.advection_upwind_1D(u=u, a=u, step_size=domain.dx[0], accuracy=3)

        rhs_diff = diffusion.diffusion_1D(u=u, diffusivity=nu, step_size=domain.dx)

        return rhs_diff - rhs_adv

# SPATIAL DISCRETIZATION
u_init = init_u(domain.coords[0], 0, nu)

nu = 0.07

out = Burgers1D.equation_of_motion(0, u_init, (nu, domain))


out.min(), out.max()

(Array(-14.83436605, dtype=float64), Array(173.49642625, dtype=float64))

fig, ax = plt.subplots(figsize=(5, 3))

ax.plot(domain.grid.squeeze(), u_init)
ax.plot(domain.grid.squeeze(), out)
plt.show()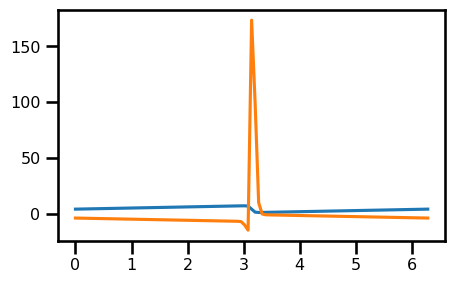

Time Stepping¶

# TEMPORAL DISCRETIZATION
# initialize temporal domain
tmin = 0.0
tmax = 0.5
num_save = 50

CFD Condition¶

# temporal parameters
c = 1.0
sigma = 0.2
nu = 0.07
dt = domain.dx[0] * nu

# SPATIAL DISCRETIZATION
u_init = init_u(domain.coords[0], 0, nu)


t_domain = TimeDomain(tmin=tmin, tmax=tmax, dt=dt)
ts = jnp.linspace(tmin, tmax, num_save)
saveat = dfx.SaveAt(ts=ts)

# DYNAMICAL SYSTEM
dyn_model = Burgers1D(t_domain=t_domain, saveat=saveat)

u_init = init_u(domain.coords[0], 0, nu)

# Euler, Constant StepSize
solver = dfx.Tsit5()
stepsize_controller = dfx.ConstantStepSize()


sol = dfx.diffeqsolve(
    terms=dfx.ODETerm(dyn_model.equation_of_motion),
    solver=solver,
    t0=ts.min(),
    t1=ts.max(),
    dt0=dt,
    y0=u_init.squeeze(),
    saveat=saveat,
    args=(nu, domain),
    stepsize_controller=stepsize_controller,
)

u_analytical = jax.vmap(init_u, in_axes=(None, 0, None))(domain.coords[0], ts, nu)
u_analytical.shape

(50, 101)

Analysis¶

da_sol = xr.DataArray(
    data=np.asarray(sol.ys),
    dims=["time", "x"],
    coords={
        "x": (["x"], np.asarray(domain.coords[0])),
        "time": (["time"], np.asarray(sol.ts)),
    },
    attrs={"pde": "linear_convection", "c": c, "sigma": sigma},
)

da_analytical = xr.DataArray(
    data=np.asarray(u_analytical),
    dims=["time", "x"],
    coords={
        "x": (["x"], np.asarray(domain.coords[0])),
        "time": (["time"], np.asarray(ts)),
    },
    attrs={"pde": "linear_convection", "c": c, "sigma": sigma},
)

fig, ax = plt.subplots(nrows=2)

da_sol.T.plot.pcolormesh(ax=ax[0], cmap="gray_r")
da_analytical.T.plot.pcolormesh(ax=ax[1], cmap="gray_r")

plt.tight_layout()
plt.show()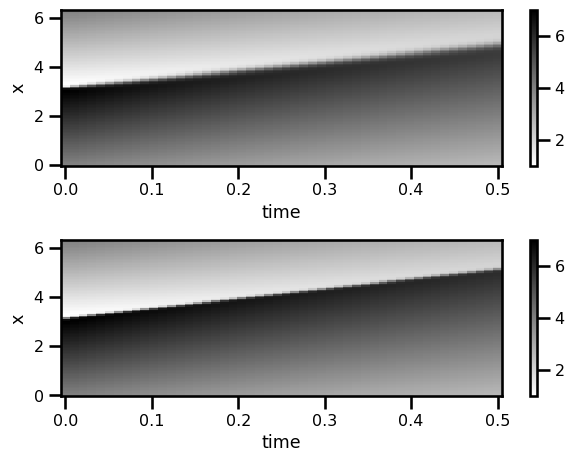

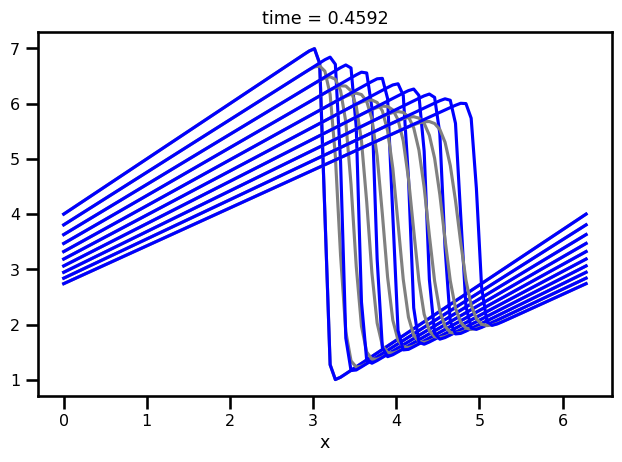
fig, ax = plt.subplots()

for i in range(0, len(da_sol.time), 5):
    da_sol.isel(time=i).plot.line(ax=ax, color="gray")
    da_analytical.isel(time=i).plot.line(ax=ax, color="blue")

plt.tight_layout()
plt.show()

12 Steps to Navier-Stokes

1D Diffusion

12 Steps to Navier-Stokes

2D Linear Convection