2D Laplace's Equation

J. Emmanuel JohnsonTakaya Uchida

This tutorial comes from the following resources:

12 Steps to Navier-Stokes - 2D Burgers -ipynb
JupyterBook on Iterative Models - jbook

My Notes:

I had some serious stability issues from the time stepper. The CFL Condition is important!
The code started to get a bit cumbersome, so I used a custom state + abstract functions.

import autoroot
import jax
import jax.numpy as jnp
import numpy as np
import numba as nb
import equinox as eqx
import kernex as kex
import finitediffx as fdx
import diffrax as dfx
import xarray as xr
import matplotlib.pyplot as plt
import seaborn as sns
from tqdm.notebook import tqdm, trange
from jaxtyping import Float, Array, PyTree, ArrayLike
import wandb
from jaxsw._src.domain.base import Domain
from jaxsw._src.models.pde import DynamicalSystem
from jaxsw._src.domain.time import TimeDomain
import lineax as lx

sns.reset_defaults()
sns.set_context(context="talk", font_scale=0.7)
jax.config.update("jax_enable_x64", True)

%matplotlib inline
%load_ext autoreload
%autoreload 2

Let's start with a simple 2D Diffusion scheme. This PDE is defined as:

\begin{aligned} \frac{\partial^2 p}{\partial x^2} + \frac{\partial^2 p}{\partial y^2} = 0 \end{aligned}

(1)

Here, we are advised to use a 2nd order accuracy central difference method.

However, this is a PDE with no time dependence. We have a minimization problem where we want the best $p$ that solves the PDE. More concretely, we have

\begin{aligned} p^* &= \underset{p}{\text{argmin }}\mathcal{U}(p) \\ &\text{s.t.}\hspace{3mm}\mathcal{U}(p):=\nabla^2p = 0 \end{aligned}

(2)

So we need to iteratively solve for this. Basically we will do:

p_0 = ...
p_* = FixedPoint(p_0)

Domain¶

nx, ny = 41, 41
xmin, ymin = 0.0, 0.0
xmax, ymax = 2.0, 1.0

domain = Domain.from_numpoints(xmin=(xmin, ymin), xmax=(xmax, ymax), N=(nx, ny))

print(f"Size: {domain.size}")
print(f"nDims: {domain.ndim}")
print(f"Grid Size: {domain.grid.shape}")
print(f"Cell Volume: {domain.cell_volume}")

Size: (40, 40)
nDims: 2
Grid Size: (40, 40, 2)
Cell Volume: 0.0012500000000000002

Initial Conditions¶

We're doing a very specific initialization which is defined as:

\begin{aligned} \mathcal{IC}[p] &= \begin{cases} 0 && \text{for }x=0\\ y && \text{for }x=2\\ \end{cases} \\ \mathcal{IC}\left[\frac{\partial p}{\partial y}\right] &= 0 && \text{for }y=0,1 \end{aligned}

(3)

def init_u0(domain):
    """Initial condition from grid"""
    u = jnp.zeros(domain.size, dtype=jnp.float64)

    y = domain.coords[1]

    u = u.at[0, :].set(0)
    u = u.at[-1, :].set(jnp.asarray(y))
    u = u.at[:, 0].set(u[:, 1])
    u = u.at[:, -1].set(u[:, -2])
    return u

u_init = init_u0(domain)

grid = domain.grid

u_init.shape

(40, 40)

from matplotlib import cm

fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
surf = ax.plot_surface(
    grid[..., 0],
    grid[..., 1],
    u_init,
    cmap=cm.coolwarm,
    # vmin=u_init.min(), vmax=u.max()+0.1*u.max()
)
plt.colorbar(surf, shrink=0.5, aspect=5)
plt.tight_layout()
plt.show()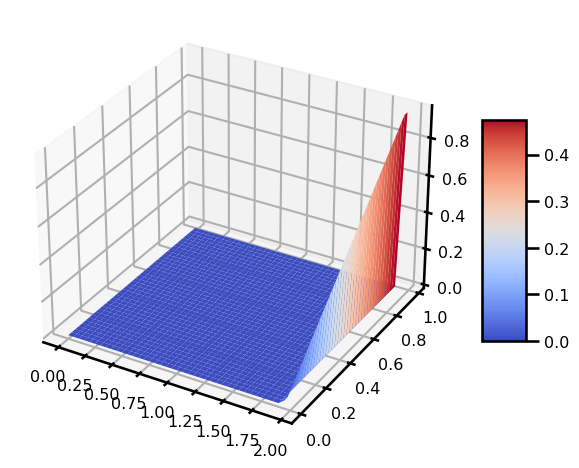

domain.size

(40, 40)

Boundary Conditions¶

We are using the same boundary conditions as before, 1's everywhere.

\begin{aligned} \mathcal{BC}[u](\mathbf{x}) = \mathcal{BC}[v](\mathbf{x})&= 1 && && \mathbf{x}\in\partial\Omega \end{aligned}

(4)

Note, we use the same BCs for both $u$ and $v$ .

def bc_fn(u: Array) -> Array:
    y = domain.coords[1]

    u = u.at[0, :].set(0)
    u = u.at[-1, :].set(jnp.asarray(y))
    u = u.at[:, 0].set(u[:, 1])
    u = u.at[:, -1].set(u[:, -2])

    return u

Equation of Motion¶

Because we are doing advection, we will use backwards difference for each of the terms.

\begin{aligned} D^-{2}_x[u] &:= \frac{\partial^2 u}{\partial x^2} \\ D^-{2}_y[u] &:= \frac{\partial^2 u}{\partial y^2} \end{aligned}

(5)

where $D^2$ is the 2nd order accurate central difference method.

It's starting to get a bit cumbersome to put everything into a single equation, so we will start making functions for each other terms.

Laplacian Equation¶

We have the advection term for both $u$ and $v$ :

\begin{aligned} \frac{\partial u}{\partial t} &+ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = 0 \\ \frac{\partial v}{\partial t} &+ u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} = 0 \end{aligned}

(6)

They recommend that we use the 1st order accurate backward difference scheme. We will make a generic advection function term that should work for both $u$ and $v$ .

from jaxsw._src.operators.functional import elliptical

Iterative Methods¶

Conditions:

Max Iterations are completed
Our criteria is met!

Steepest Descent¶

from jaxsw._src.utils.linear_solver import steepest_descent
import functools as ft

target_criterion = 1e-6
max_iterations = 100_000
criterion = "l2"
u = init_u0(domain).copy()
b = jnp.zeros_like(u)

matvec_fn = ft.partial(elliptical.laplacian_matvec, step_size=domain.dx, bc_fn=bc_fn)


out = steepest_descent(
    b=b,
    matvec_fn=matvec_fn,
    u_init=u,
    target_criterion=target_criterion,
    max_iterations=max_iterations,
    criterion=criterion,
)
out.iteration, out.loss

(Array(100000, dtype=int64, weak_type=True),
 Array(1.36352081e-05, dtype=float64))

from matplotlib import cm

fig, ax = plt.subplots(ncols=2, figsize=(15, 5), subplot_kw={"projection": "3d"})

surf = ax[0].plot_surface(grid[..., 0], grid[..., 1], u, cmap=cm.coolwarm)
plt.colorbar(surf, shrink=0.5, aspect=5)
surf = ax[1].plot_surface(grid[..., 0], grid[..., 1], out.u, cmap=cm.coolwarm)
plt.colorbar(surf, shrink=0.5, aspect=5)
plt.tight_layout()
plt.show()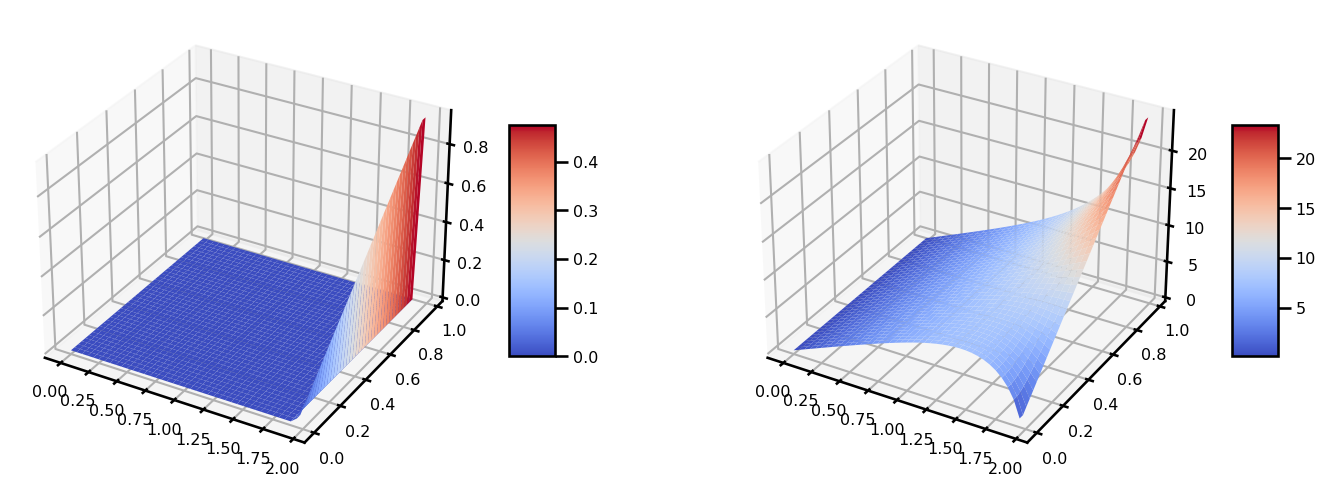

Conjugate Gradient (From Scratch)¶

from jaxsw._src.utils.linear_solver import steepest_descent, conjugate_gradient
import functools as ft

target_criterion = 1e-5
max_iterations = 2_000
criterion = "l2"
u = init_u0(domain).copy()
b = jnp.zeros_like(u)

matvec_fn = ft.partial(elliptical.laplacian_matvec, step_size=domain.dx, bc_fn=bc_fn)


out = conjugate_gradient(
    b=b,
    matvec_fn=matvec_fn,
    u_init=u,
    target_criterion=target_criterion,
    max_iterations=max_iterations,
    criterion=criterion,
)
out.iteration, out.loss

(Array(1000, dtype=int64, weak_type=True), Array(0.01606126, dtype=float64))

from matplotlib import cm

fig, ax = plt.subplots(ncols=2, figsize=(15, 5), subplot_kw={"projection": "3d"})

surf = ax[0].plot_surface(grid[..., 0], grid[..., 1], u, cmap=cm.coolwarm)
plt.colorbar(surf, shrink=0.5, aspect=5)
surf = ax[1].plot_surface(grid[..., 0], grid[..., 1], out.u, cmap=cm.coolwarm)
plt.colorbar(surf, shrink=0.5, aspect=5)
plt.tight_layout()
plt.show()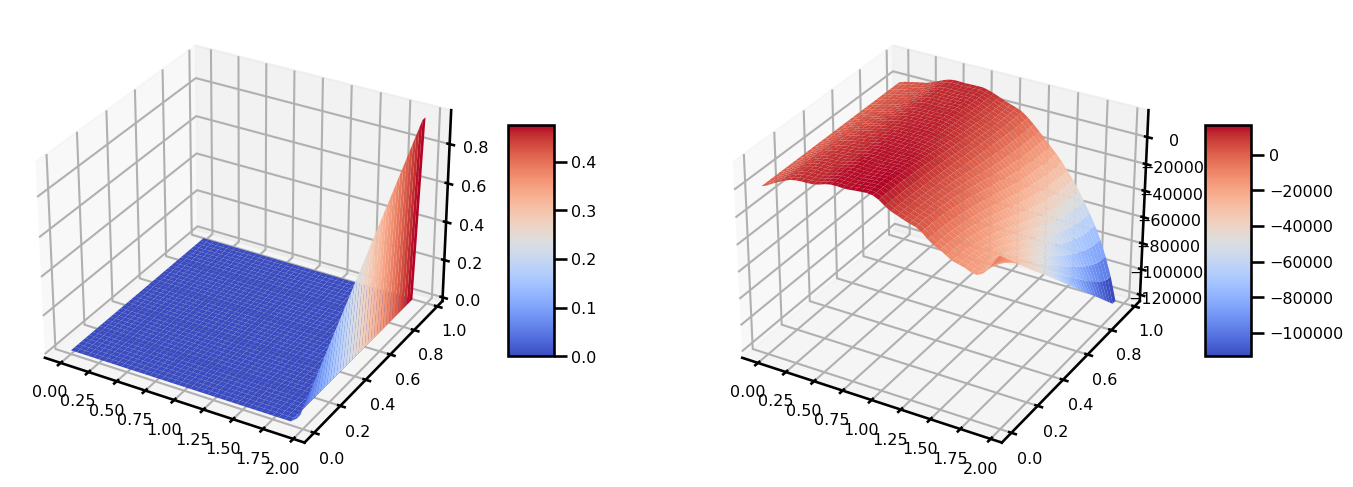

`JaxOpt`¶

This is a general purpose optimization package using the JAX framework.

import typing as tp
from jaxopt import linear_solve
from jaxsw._src.utils.linear_solver import jaxopt_linear_solver


# define initial state
u_init = init_u0(domain).copy()

# define RHS
b = jnp.zeros_like(u_init)

# define solver
solver = linear_solve.solve_cg  # BiCGStab, NormalCG, GMRES, CG
solver_kwargs = dict(maxiters=10_000, tol=1e-5)

# create matvec_fn
matvec_fn = ft.partial(elliptical.laplacian_matvec, step_size=domain.dx, bc_fn=bc_fn)

# get solution
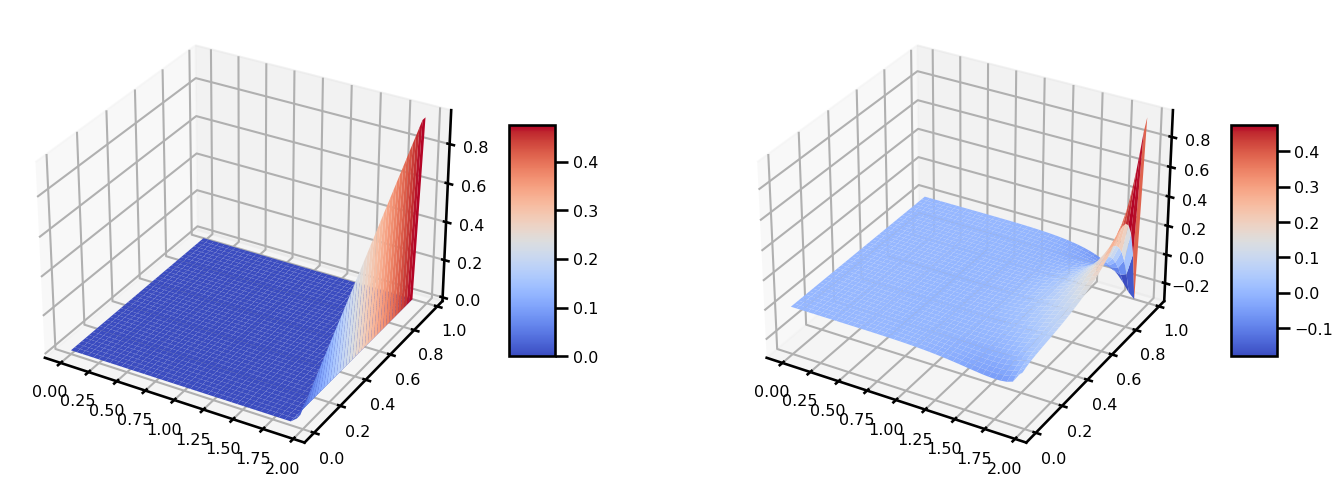
u_out = jaxopt_linear_solver(matvec_fn=matvec_fn, b=b, solver=solver)

from matplotlib import cm

fig, ax = plt.subplots(ncols=2, figsize=(15, 5), subplot_kw={"projection": "3d"})
surf = ax[0].plot_surface(grid[..., 0], grid[..., 1], u_init, cmap=cm.coolwarm)
plt.colorbar(surf, shrink=0.5, aspect=5)
surf = ax[1].plot_surface(grid[..., 0], grid[..., 1], u_out, cmap=cm.coolwarm)
plt.colorbar(surf, shrink=0.5, aspect=5)
plt.tight_layout()
plt.show()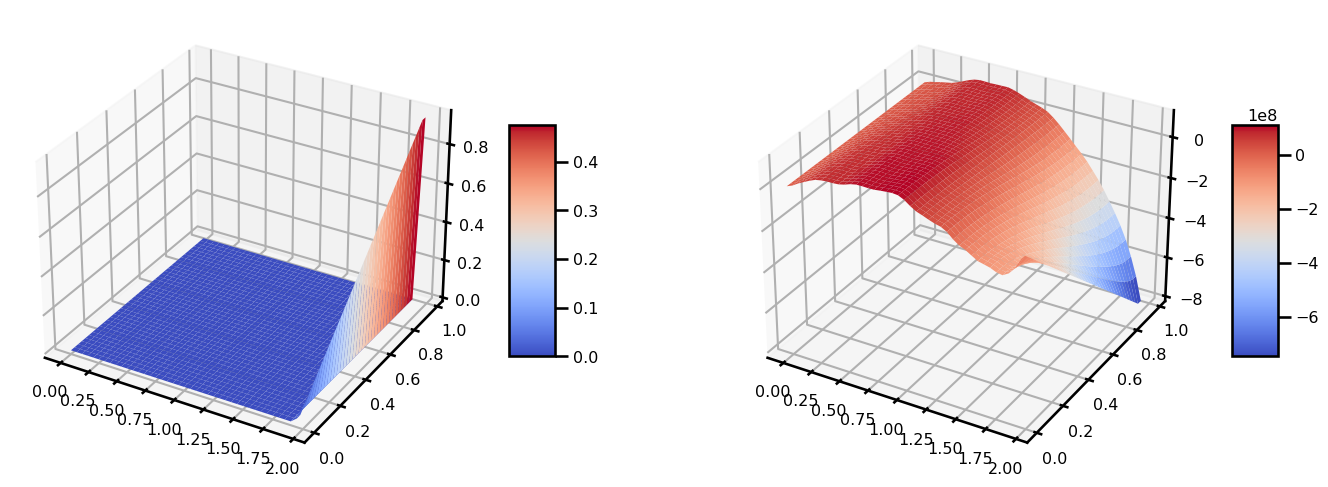

`Lineax`¶

This is a fairly new package that came out which does some linear solvers using the equinox framework.

import typing as tp
from jaxsw._src.utils.linear_solver import lx_linear_solver


# define initial state
u_init = init_u0(domain).copy()

# define RHS
b = jnp.zeros_like(u_init)

# define solver
solver = lx.NormalCG(rtol=1e-6, atol=1e-6)  # BiCGStab, NormalCG, GMRES, CG

# create matvec_fn
matvec_fn = ft.partial(elliptical.laplacian_matvec, step_size=domain.dx, bc_fn=bc_fn)

# get solution
u_out = lx_linear_solver(matvec_fn, b, solver=solver, verbose=True)

{'max_steps': None, 'num_steps': Array(1519, dtype=int64)}

from matplotlib import cm

fig, ax = plt.subplots(ncols=2, figsize=(15, 5), subplot_kw={"projection": "3d"})
surf = ax[0].plot_surface(grid[..., 0], grid[..., 1], u_init, cmap=cm.coolwarm)
plt.colorbar(surf, shrink=0.5, aspect=5)
surf = ax[1].plot_surface(grid[..., 0], grid[..., 1], u_out, cmap=cm.coolwarm)
plt.colorbar(surf, shrink=0.5, aspect=5)
plt.tight_layout()
plt.show()

12 Steps to Navier-Stokes

2D Burgers Equation