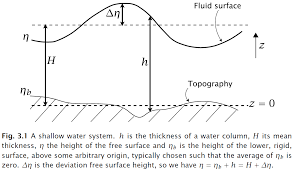
Shallow Water ¶ Figure 1: The shallow water equations schematic as per [Vallis, 2019
h ( x , y , t ) = η ( x , y , t ) − η B ( x , y , t ) h(x,y,t) = \eta(x,y,t) - \eta_B(x,y,t) h ( x , y , t ) = η ( x , y , t ) − η B ( x , y , t ) where h h h η \eta η η B \eta_B η B Note : when the lower surface is completely flat, then η B \eta_B η B h = η h=\eta h = η η 2 \eta_2 η 2 η B \eta_B η B
We can also define the layer thickness to be a function of the surface displacement and mean height as
h ( x , y , t ) = η ( x , y , t ) + H ( x , y ) h(x,y,t) = \eta(x,y,t) + H(x,y) h ( x , y , t ) = η ( x , y , t ) + H ( x , y ) where H H H
η = h + η B = H + η T \eta = h + \eta_B = H + \eta_T η = h + η B = H + η T where η T \eta_T η T
For the SW equations, we define a PDE that captures spatiotemporal relationships between the total thickness height, h h h ( u , v ) (u,v) ( u , v )
Height : h = h ( x ⃗ , t ) x ⃗ ∈ Ω ⊂ R D s , t ∈ T ⊂ R + Zonal Velocity : u = u ( x ⃗ , t ) x ⃗ ∈ Ω ⊂ R D s , t ∈ T ⊂ R + Meridonal Velocity : v = v ( x ⃗ , t ) x ⃗ ∈ Ω ⊂ R D s , t ∈ T ⊂ R + \begin{aligned}
\text{Height}: &&
h & =\boldsymbol{h}(\vec{\mathbf{x}},t) && &&
\vec{\mathbf{x}}\in\Omega\sub\mathbb{R}^{D_s} , &&
t\in\mathcal{T}\sub\mathbb{R}^{+} \\
\text{Zonal Velocity}: &&
u & =\boldsymbol{u}(\vec{\mathbf{x}},t) && &&
\vec{\mathbf{x}}\in\Omega\sub\mathbb{R}^{D_s} , &&
t\in\mathcal{T}\sub\mathbb{R}^{+} \\
\text{Meridonal Velocity}: &&
v & =\boldsymbol{v}(\vec{\mathbf{x}},t) && &&
\vec{\mathbf{x}}\in\Omega\sub\mathbb{R}^{D_s}, &&
t\in\mathcal{T}\sub\mathbb{R}^{+} \\
\end{aligned} Height : Zonal Velocity : Meridonal Velocity : h u v = h ( x , t ) = u ( x , t ) = v ( x , t ) x ∈ Ω ⊂ R D s , x ∈ Ω ⊂ R D s , x ∈ Ω ⊂ R D s , t ∈ T ⊂ R + t ∈ T ⊂ R + t ∈ T ⊂ R + We can write out the momentum constraints for the velocity vector-field, u ⃗ \vec{\boldsymbol{u}} u h h h SW equations as
Momentum : D t u ⃗ + f × u ⃗ = − g ∇ ( h + η B ) Mass : ∂ t h + ∇ ⋅ ( h u ⃗ ) = 0 \begin{aligned}
\text{Momentum}: && &&
D_t\vec{\boldsymbol{u}} + f\times \vec{\boldsymbol{u}} &=
- g \boldsymbol{\nabla}(h + \eta_B) \\
\text{Mass}: && &&
\partial_t h +
\boldsymbol{\nabla}\cdot(h\vec{\boldsymbol{u}}) &=
0
\end{aligned} Momentum : Mass : D t u + f × u ∂ t h + ∇ ⋅ ( h u ) = − g ∇ ( h + η B ) = 0 where h u ⃗ h\vec{\boldsymbol{u}} h u f f f (28) g g g
Height : ∂ t h + ∂ x ( h u ) + ∂ y ( h v ) = 0 Zonal Velocity : ∂ t u + u ∂ x u + v ∂ y u − f v = − g ∂ x ( h + η B ) + F x + B x + M x + ξ x Meridonal Velocity : ∂ t v + u ∂ x v + v ∂ y v + f u = − g ∂ y ( h + η B ) + F y + B y + M y + ξ y \begin{aligned}
\text{Height}: && &&
\partial_t h +
\partial_x (hu) + \partial_y (hv) &= 0\\
\text{Zonal Velocity}: && &&
\partial_t u +
u \partial_x u + v\partial_y u - fv &=
- g \partial_x (h + \eta_B) + F_x + B_x + M_x + \xi_x \\
\text{Meridonal Velocity}: && &&
\partial_t v +
u \partial_x v + v\partial_y v + fu &=
- g \partial_y (h + \eta_B) + F_y + B_y + M_y + \xi_y
\end{aligned} Height : Zonal Velocity : Meridonal Velocity : ∂ t h + ∂ x ( h u ) + ∂ y ( h v ) ∂ t u + u ∂ x u + v ∂ y u − f v ∂ t v + u ∂ x v + v ∂ y v + f u = 0 = − g ∂ x ( h + η B ) + F x + B x + M x + ξ x = − g ∂ y ( h + η B ) + F y + B y + M y + ξ y We have a lot of extra terms in the above equation as was proposed in [Klöwer et al. , 2018
Forcing Terms ¶ There is a forcing vector which operates on the ( x , y ) (x,y) ( x , y ) f ⃗ : Ω × T → R 2 \vec{\boldsymbol{f}}:\Omega\times\mathcal{T} \rightarrow \mathbb{R}^{2} f : Ω × T → R 2 (6)
f ⃗ = [ F x , F y ] ⊤ = [ F x ( x ⃗ , t ) , F y ( x ⃗ , t ) ] ⊤ \vec{\boldsymbol{f}} =
[F_x, F_y]^\top =
\left[
\boldsymbol{F}_x(\vec{\boldsymbol{x}},t),
\boldsymbol{F}_y(\vec{\boldsymbol{x}},t)
\right]^\top f = [ F x , F y ] ⊤ = [ F x ( x , t ) , F y ( x , t ) ] ⊤ This forcing operates on the top of the model, for example the wind or atmospheric component.
Bottom Friction Term ¶ b ⃗ = [ B x , B y ] ⊤ = [ B x ( u ⃗ , h ) , B y ( u ⃗ , h ) ] ⊤ \vec{\boldsymbol{b}} =
[B_x, B_y]^\top =
\left[
\boldsymbol{B}_x(\vec{\boldsymbol{u}},h),
\boldsymbol{B}_y(\vec{\boldsymbol{u}},h)
\right]^\top b = [ B x , B y ] ⊤ = [ B x ( u , h ) , B y ( u , h ) ] ⊤ Lateral Mixing of Momentum ¶ m ⃗ = [ M x , M y ] ⊤ = [ M x ( u ⃗ , h ) , M y ( u ⃗ , h ) ] ⊤ \vec{\boldsymbol{m}} =
[M_x, M_y]^\top =
\left[
\boldsymbol{M}_x(\vec{\boldsymbol{u}},h),
\boldsymbol{M}_y(\vec{\boldsymbol{u}},h)
\right]^\top m = [ M x , M y ] ⊤ = [ M x ( u , h ) , M y ( u , h ) ] ⊤ Negative Viscosity Backscatter ¶ Ξ ⃗ = [ ξ x , ξ y ] ⊤ \vec{\boldsymbol{\Xi}} = [\xi_x, \xi_y]^\top Ξ = [ ξ x , ξ y ] ⊤ We can rewrite the formulation for the momentum parts, ( u , v ) (u,v) ( u , v ) (6)
∂ t u ⃗ + u ⃗ ⋅ ∇ u ⃗ + f × u ⃗ = − g ∇ h \partial_t \vec{\boldsymbol{u}} +
\vec{\boldsymbol{u}} \cdot \boldsymbol{\nabla} \vec{\boldsymbol{u}}
+ f\times \vec{\boldsymbol{u}} =
- g \boldsymbol{\nabla}h ∂ t u + u ⋅ ∇ u + f × u = − g ∇ h We will use the vector identity of equation (33) (11)
Height : ∂ t h = − ∂ x ( h u ) − ∂ y ( h v ) = 0 Zonal Velocity : ∂ t u = q h v − ∂ x p + F x + M x + B x + ξ x Meridonal Velocity : ∂ t v = − q h u − ∂ y p + F y + M y + B y + ξ y \begin{aligned}
\text{Height}: && &&
\partial_t h &=
-\partial_x (hu) - \partial_y (hv) = 0\\
\text{Zonal Velocity}: && &&
\partial_t u &=
qhv - \partial_x p + F_x + M_x + B_x + \xi_x \\
\text{Meridonal Velocity}: && &&
\partial_t v
&= - qhu - \partial_y p + F_y + M_y + B_y + \xi_y
\end{aligned} Height : Zonal Velocity : Meridonal Velocity : ∂ t h ∂ t u ∂ t v = − ∂ x ( h u ) − ∂ y ( h v ) = 0 = q h v − ∂ x p + F x + M x + B x + ξ x = − q h u − ∂ y p + F y + M y + B y + ξ y where q q q (30) p p p (32)
We will walk through the entire derivation.
Let's rewrite all of the terms
∂ t u ⃗ + u ⃗ ⋅ ∇ u ⃗ + f × u ⃗ = − g ∇ h \partial_t \vec{\boldsymbol{u}} +
\vec{\boldsymbol{u}} \cdot \boldsymbol{\nabla} \vec{\boldsymbol{u}}
+ f\times \vec{\boldsymbol{u}} =
- g \boldsymbol{\nabla}h ∂ t u + u ⋅ ∇ u + f × u = − g ∇ h We will use the vector identity in equation (33) (11)
∂ t u ⃗ + ( ∇ × u ⃗ ) × u ⃗ + 1 2 ∇ ( u ⃗ ⋅ u ⃗ ) + f × u ⃗ = − g ∇ h \partial_t \vec{\boldsymbol{u}} +
(\boldsymbol{\nabla}\times \vec{\boldsymbol{u}})\times
\vec{\boldsymbol{u}} +
\frac{1}{2}\boldsymbol{\nabla}(\vec{\boldsymbol{u}} \cdot \vec{\boldsymbol{u}})
+ f\times \vec{\boldsymbol{u}} =
- g \boldsymbol{\nabla}h ∂ t u + ( ∇ × u ) × u + 2 1 ∇ ( u ⋅ u ) + f × u = − g ∇ h We will rearrange the equation to isolate the curl portions
∂ t u ⃗ + ( ∇ × u ⃗ ) × u ⃗ + f × u ⃗ = − g ∇ h − 1 2 ∇ ( u ⃗ ⋅ u ⃗ ) \partial_t \vec{\boldsymbol{u}} +
(\boldsymbol{\nabla}\times \vec{\boldsymbol{u}})\times
\vec{\boldsymbol{u}} +
f\times \vec{\boldsymbol{u}} =
- g \boldsymbol{\nabla}h -
\frac{1}{2}\boldsymbol{\nabla}(\vec{\boldsymbol{u}} \cdot \vec{\boldsymbol{u}}) ∂ t u + ( ∇ × u ) × u + f × u = − g ∇ h − 2 1 ∇ ( u ⋅ u ) Now, we will collapse all like terms
∂ t u ⃗ + ( ∇ × u ⃗ + f ) × u ⃗ = − g ∇ ( h + 1 2 u ⃗ ⋅ u ⃗ ) \partial_t \vec{\boldsymbol{u}} +
(\boldsymbol{\nabla}\times \vec{\boldsymbol{u}} + f)\times \vec{\boldsymbol{u}} =
- g \boldsymbol{\nabla} \left(h +
\frac{1}{2}\vec{\boldsymbol{u}} \cdot \vec{\boldsymbol{u}}\right) ∂ t u + ( ∇ × u + f ) × u = − g ∇ ( h + 2 1 u ⋅ u ) We will use the definition of relative vorticity, ζ \zeta ζ (29)
∂ t u ⃗ + ( ζ + f ) × u ⃗ = − g ∇ ( h + 1 2 u ⃗ ⋅ u ⃗ ) \partial_t \vec{\boldsymbol{u}} +
(\zeta + f)\times \vec{\boldsymbol{u}} =
- g \boldsymbol{\nabla} \left(h +
\frac{1}{2}\vec{\boldsymbol{u}} \cdot \vec{\boldsymbol{u}}\right) ∂ t u + ( ζ + f ) × u = − g ∇ ( h + 2 1 u ⋅ u ) Now, we will use the definition of potential vorticity in the context of the height (equation (30) h h \frac{h}{h} h h
∂ t u ⃗ + ( q h ) × u ⃗ = − g ∇ ( h + 1 2 u ⃗ ⋅ u ⃗ ) \partial_t \vec{\boldsymbol{u}} +
(qh)\times \vec{\boldsymbol{u}} =
- g \boldsymbol{\nabla} \left(h +
\frac{1}{2}\vec{\boldsymbol{u}} \cdot \vec{\boldsymbol{u}}\right) ∂ t u + ( q h ) × u = − g ∇ ( h + 2 1 u ⋅ u ) Now, we can expand the curl term to be
∂ t u ⃗ + q h u ⃗ = − g ∇ ( h + 1 2 u ⃗ ⋅ u ⃗ ) \partial_t \vec{\boldsymbol{u}} +
qh\vec{\boldsymbol{u}} =
- g \boldsymbol{\nabla} \left(h +
\frac{1}{2}\vec{\boldsymbol{u}} \cdot \vec{\boldsymbol{u}}\right) ∂ t u + q h u = − g ∇ ( h + 2 1 u ⋅ u ) So we can rewrite the full formulas as
Height : ∂ t h = − ∂ x ( h u ) − ∂ y ( h v ) = 0 Zonal Velocity : ∂ t u = q h v − ∂ x ( g ( h + η B ) + 1 2 ( u 2 + v 2 ) ) Meridonal Velocity : ∂ t v = − q h u − ∂ y ( g ( h + η B ) + 1 2 ( u 2 + v 2 ) ) \begin{aligned}
\text{Height}: && &&
\partial_t h &=
-\partial_x (hu) - \partial_y (hv) = 0\\
\text{Zonal Velocity}: && &&
\partial_t u &=
qhv
- \partial_x \left(g(h + \eta_B) + \frac{1}{2}(u^2 + v^2) \right) \\
\text{Meridonal Velocity}: && &&
\partial_t v
&= - qhu
- \partial_y\left(g(h + \eta_B) + \frac{1}{2}(u^2 + v^2)\right)
\end{aligned} Height : Zonal Velocity : Meridonal Velocity : ∂ t h ∂ t u ∂ t v = − ∂ x ( h u ) − ∂ y ( h v ) = 0 = q h v − ∂ x ( g ( h + η B ) + 2 1 ( u 2 + v 2 ) ) = − q h u − ∂ y ( g ( h + η B ) + 2 1 ( u 2 + v 2 ) ) where q q q g ( h + η B ) + 1 2 ( u 2 + v 2 ) g(h + \eta_B) + \frac{1}{2}(u^2 + v^2) g ( h + η B ) + 2 1 ( u 2 + v 2 ) (32)
Linearized Shallow Water Equations ¶ We can remove the advection terms from equation (6) linearizing the PDE .
∂ t h + H ( ∂ x u + ∂ y v ) = 0 ∂ t u − f v = − g ∂ x h − κ u ∂ t v + f u = − g ∂ y h − κ v \begin{aligned}
\partial_t h &+ H
\left(\partial_x u + \partial_y v \right) = 0 \\
\partial_t u &- fv =
- g \partial_x h
- \kappa u \\
\partial_t v &+ fu =
- g \partial_y h
- \kappa v
\end{aligned} ∂ t h ∂ t u ∂ t v + H ( ∂ x u + ∂ y v ) = 0 − f v = − g ∂ x h − κ u + f u = − g ∂ y h − κ v This is appropriate for when the Rossby number is small.
We also assume that the wave height is much smaller than the actual mean height.
Example Applications ¶ Data Assimilation ¶ This has been used in data assimilation schemes [Guillou et al. , 2021 QG model was used for the balanced motions and a linear SW mode was used for the internal tides.
Wind Forcing ¶ We can construct a very typical wind forcing system that is typical within the Northern Hemisphere at mid-latitudes.
It will resemble the tradewinds in the southern part of the domain and the westerlies in the northern part.
We first define a domain with a height, H H H ( L x , L y ) (L_x,L_y) ( L x , L y )
F y = 0 F x = F 0 ρ 0 H [ cos ( 2 π ( 2 L y − 1 2 ) ) + 2 sin ( 2 π ( y L y − 1 2 ) ) ] \begin{aligned}
F_y &= 0 \\
F_x &= \frac{F_0}{\rho_0 H}
\left[
\cos \left( 2\pi \left(\frac{2}{L_y} - \frac{1}{2} \right)\right) +
2\sin \left(2\pi \left( \frac{y}{L_y} - \frac{1}{2} \right) \right)
\right]
\end{aligned} F y F x = 0 = ρ 0 H F 0 [ cos ( 2 π ( L y 2 − 2 1 ) ) + 2 sin ( 2 π ( L y y − 2 1 ) ) ] where F 0 = 0.12 F_0=0.12 F 0 = 0.12 ρ 0 = 1 e 3 \rho_0=1e3 ρ 0 = 1 e 3 − 3 ^{-3} − 3
Boundary Conditions ¶ Kinematic Boundaries .
These boundaries prevent and flow from going through the boundaries.
These are typically on the East-West extent as the flow moves from left/right to right/left
u ( x = 0 ) = u ( x = L x ) = 0 v ( x = 0 ) = v ( x = L y ) = 0 \begin{aligned}
u(x=0)=u(x=L_x)&=0 \\
v(x=0)=v(x=L_y)&=0
\end{aligned} u ( x = 0 ) = u ( x = L x ) v ( x = 0 ) = v ( x = L y ) = 0 = 0 Gradient Boundaries .
We can also say that there is no gradient across the boundaries for the height, h h h
∂ x h ( x = 0 ) = ∂ x h ( x = L x ) = 0 ∂ y h ( x = 0 ) = ∂ y h ( x = L y ) = 0 \begin{aligned}
\partial_x h(x=0)=\partial_x h(x=L_x)&=0 \\
\partial_y h(x=0)=\partial_y h(x=L_y)&=0
\end{aligned} ∂ x h ( x = 0 ) = ∂ x h ( x = L x ) ∂ y h ( x = 0 ) = ∂ y h ( x = L y ) = 0 = 0 No-Slip Boundaries .
These refer to the idea that the tangential velocity should vanish.
We typically prescribe these for the North-South extent.
u ( y = 0 ) = u ( y = L y ) = 0 v ( y = 0 ) = v ( y = L x ) = 0 \begin{aligned}
u(y=0)=u(y=L_y)&=0 \\
v(y=0)=v(y=L_x)&=0
\end{aligned} u ( y = 0 ) = u ( y = L y ) v ( y = 0 ) = v ( y = L x ) = 0 = 0 Free-Slip Boundaries .
These refer to the idea that the tangential velocity gradients should be zero.
We often refer to these as friction-less boundaries.
We also typically prescribe these on the North-South extent.
∂ y u ( y = 0 ) = ∂ y u ( y = L y ) = 0 ∂ x v ( x = 0 ) = ∂ x v ( x = L x ) = 0 \begin{aligned}
\partial_y u(y=0)=\partial_y u(y=L_y)&=0 \\
\partial_x v(x=0)=\partial_x v(x=L_x)&=0
\end{aligned} ∂ y u ( y = 0 ) = ∂ y u ( y = L y ) ∂ x v ( x = 0 ) = ∂ x v ( x = L x ) = 0 = 0 Material Derivative ¶ This is an operator that models the movement of a fluid parcel within a Eulerian framework.
D t = ∂ t + u ⃗ ⋅ ∇ = ∂ t + u ∂ x + v ∂ y D_t = \partial_t +
\vec{\boldsymbol{u}} \cdot \boldsymbol{\nabla} =
\partial_t + u\partial_x + v\partial_y D t = ∂ t + u ⋅ ∇ = ∂ t + u ∂ x + v ∂ y Planetary Vorticity ¶ f ( y ) = 2 Ω sin ( θ ) + 1 R 2 Ω cos ( θ ) y f(y) = 2\Omega\sin(\theta) + \frac{1}{R}2\Omega\cos(\theta) y f ( y ) = 2Ω sin ( θ ) + R 1 2Ω cos ( θ ) y where f 0 = 2 Ω sin ( θ 0 ) f_0=2\Omega\sin(\theta_0) f 0 = 2Ω sin ( θ 0 ) β = 1 R 2 Ω cos ( θ 0 ) \beta=\frac{1}{R}2\Omega\cos(\theta_0) β = R 1 2Ω cos ( θ 0 ) β \beta β wiki article for a better overview or this video for a more in-depth overview.
Relative Vorticity ¶ ζ = ∂ x v − ∂ y u = ∇ × u ⃗ \zeta =
\partial_x v - \partial_y u =
\boldsymbol{\nabla}\times\vec{\boldsymbol{u}} ζ = ∂ x v − ∂ y u = ∇ × u Potential Vorticity ¶ q = ζ + f h q = \frac{\zeta + f}{h} q = h ζ + f where ζ \zeta ζ (29) f f f (28) youtube video .
Kinetic Energy ¶ K E = 1 2 ( u 2 + v 2 ) \mathcal{KE} = \frac{1}{2}\left( u^2 + v^2\right) K E = 2 1 ( u 2 + v 2 ) Bernoulli Potential ¶ Bernoulli Potential : p = 1 2 ( u 2 + v 2 ) + g ( h + η B ) = K E + g ( h + η B ) \begin{aligned}
\text{Bernoulli Potential}: && &&
p &= \frac{1}{2}(u^2 + v^2) + g (h + \eta_B) = \mathcal{KE} + g(h + \eta_B)
\end{aligned} Bernoulli Potential : p = 2 1 ( u 2 + v 2 ) + g ( h + η B ) = K E + g ( h + η B ) Vector Identity ¶ u ⃗ ⋅ ∇ u ⃗ = ( ∇ × u ⃗ ) × u ⃗ + 1 2 ∇ ( u ⃗ ⋅ u ⃗ ) \vec{\boldsymbol{u}} \cdot \boldsymbol{\nabla}\vec{\boldsymbol{u}} =
(\boldsymbol{\nabla}\times \vec{\boldsymbol{u}})\times
\vec{\boldsymbol{u}} +
\frac{1}{2}\boldsymbol{\nabla}(\vec{\boldsymbol{u}} \cdot \vec{\boldsymbol{u}}) u ⋅ ∇ u = ( ∇ × u ) × u + 2 1 ∇ ( u ⋅ u )