Jax Approximate Ocean Models

Linear Shallow Water Model - Rossby Example

Authors

Affiliations

J. Emmanuel Johnson

CNRS

MEOM

Takaya Uchida

FSU

import autoroot
import jax
import jax.numpy as jnp
import numpy as np
import equinox as eqx
import kernex as kex
import finitediffx as fdx
import diffrax as dfx
import xarray as xr
import matplotlib.pyplot as plt
import seaborn as sns
import typing as tp
from tqdm.notebook import tqdm, trange
from jaxtyping import Float, Array, PyTree, ArrayLike
import pandas as pd
from jaxsw._src.domain.base import Domain
from jaxsw._src.models.pde import DynamicalSystem
from jaxsw._src.domain.time import TimeDomain
from jaxsw._src.operators.functional import grid as F_grid
from jaxsw._src.models.sw import Params as SWMParams, State as SWMState
from jaxsw._src.models.sw.linear import LinearShallowWater2D

sns.reset_defaults()
sns.set_context(context="talk", font_scale=0.7)
jax.config.update("jax_enable_x64", True)

%matplotlib inline
%load_ext autoreload
%autoreload 2

Formulation¶

\begin{aligned} \frac{\partial h}{\partial t} &+ H \left(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \right) = 0 \\ \frac{\partial u}{\partial t} &- fv = - g \frac{\partial h}{\partial x} - \kappa u \\ \frac{\partial v}{\partial t} &+ fu = - g \frac{\partial h}{\partial y} - \kappa v \end{aligned}

(1)

State¶

Here, we have 3 fields we have to content with:

$h$ - height
$u$ - u-velocity (zonal velocity)
$v$ - v-velocity (meridonal velocity)

So our state will be a container for each of these fields.

SWMState??

Init signature: SWMState(u: jax.Array, v: jax.Array, h: jax.Array)
Docstring:      State(u, v, h)
Source:        
class State(tp.NamedTuple):
    u: Array
    v: Array
    h: Array

    @classmethod
    def init_state(cls, params, init_h=None, init_v=None, init_u=None):
        h = init_h(params) if init_h is not None else State.zero_init(params.domain)
        v = init_v(params) if init_v is not None else State.zero_init(params.domain)
        u = init_u(params) if init_u is not None else State.zero_init(params.domain)
        return cls(u=u, v=v, h=h)

    @staticmethod
    def zero_init(domain):
        return jnp.zeros_like(domain.grid[..., 0])
File:           ~/code_projects/jaxsw/jaxsw/_src/models/sw/__init__.py
Type:           type
Subclasses:

Domain¶

For the domain, we will use a generic domain for each of the variables.

dx = dy = 20e3
Lx = 100 * dx
Ly = 101 * dy


domain = Domain(xmin=(0, 0), xmax=(Lx, Ly), dx=(dx, dy))

print(f"Nx: {domain.Nx}")
print(f"Lx: {domain.Lx}")
print(f"dx: {domain.dx}")
print(f"Size: {domain.size}")
print(f"nDims: {domain.ndim}")
print(f"Grid Size: {domain.grid.shape}")
print(f"Cell Volume: {domain.cell_volume:_}")

Nx: (101, 102)
Lx: (2000000.0, 2020000.0)
dx: (20000.0, 20000.0)
Size: (101, 102)
nDims: 2
Grid Size: (101, 102, 2)
Cell Volume: 400_000_000.0

Initial Condition¶

Note: The initial condition depends on a few parameters that will also be used in other examples. So we can make the parameters container to hold all of the parameters needed.

def init_h0(params):
    """A LOT of work for a lil Gauss bump!"""
    domain = params.domain

    X = domain.grid[..., 0]
    Y = domain.grid[..., 1]

    x_center = domain.coords[0][domain.Nx[0] // 2]
    y_center = domain.coords[1][domain.Nx[1] - 2]

    h0 = params.depth + 1.0 * np.exp(
        -((X - x_center) ** 2) / params.rossby_radius(domain) ** 2
        - (Y - y_center) ** 2 / params.rossby_radius(domain) ** 2
    )

    return jnp.asarray(h0)

SWMParams??

Init signature:
SWMParams(
    domain: jaxsw._src.domain.base.Domain,
    depth: float,
    gravity: float,
    coriolis_f0: float,
    coriolis_beta: float,
)
Docstring:      Params(domain, depth, gravity, coriolis_f0, coriolis_beta)
Source:        
class Params(tp.NamedTuple):
    domain: Domain
    depth: float
    gravity: float
    coriolis_f0: float  # or ARRAY
    coriolis_beta: float  # or ARRAY

    @property
    def phase_speed(self):
        return jnp.sqrt(self.gravity * self.depth)

    def rossby_radius(self, domain):
        return self.phase_speed / self.coriolis_param(domain).mean()
        # return self.phase_speed / self.coriolis_f0

    def coriolis_param(self, domain):
        return self.coriolis_f0 + domain.grid[..., 1] * self.coriolis_beta

    def lateral_viscosity(self, domain):
        return 1e-3 * self.coriolis_f0 * domain.dx[0] ** 2
File:           ~/code_projects/jaxsw/jaxsw/_src/models/sw/__init__.py
Type:           type
Subclasses:

params = SWMParams(
    depth=100.0, gravity=9.81, coriolis_f0=2e-4, coriolis_beta=2e-11, domain=domain
)

h0 = init_h0(params)

plt.imshow(h0, cmap="RdBu_r")

<matplotlib.image.AxesImage at 0x17dedecd0>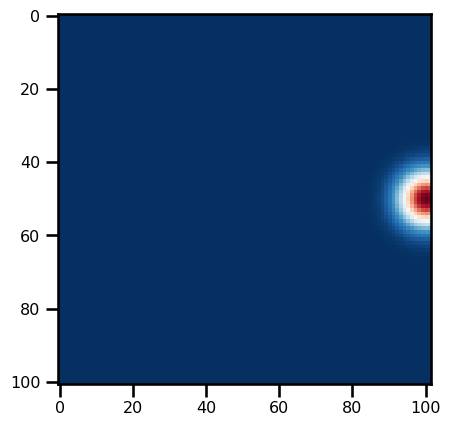

State Revisited¶

Now that we have an initial condition for each of the variables, we can make a small convenience function for the state so that we can initialize it using our initial conditions. This will make our container more complete

SWMState??

Init signature: SWMState(u: jax.Array, v: jax.Array, h: jax.Array)
Docstring:      State(u, v, h)
Source:        
class State(tp.NamedTuple):
    u: Array
    v: Array
    h: Array

    @classmethod
    def init_state(cls, params, init_h=None, init_v=None, init_u=None):
        h = init_h(params) if init_h is not None else State.zero_init(params.domain)
        v = init_v(params) if init_v is not None else State.zero_init(params.domain)
        u = init_u(params) if init_u is not None else State.zero_init(params.domain)
        return cls(u=u, v=v, h=h)

    @staticmethod
    def zero_init(domain):
        return jnp.zeros_like(domain.grid[..., 0])
File:           ~/code_projects/jaxsw/jaxsw/_src/models/sw/__init__.py
Type:           type
Subclasses:

state_init = SWMState.init_state(params, init_h0)

fig, ax = plt.subplots(ncols=3, figsize=(10, 5))
ax[0].imshow(state_init.h.T, origin="lower", cmap="RdBu_r")
ax[0].set(title="h")

ax[1].imshow(state_init.u.T, origin="lower", cmap="RdBu_r")
ax[1].set(title="u-velocity")

ax[2].imshow(state_init.v.T, origin="lower", cmap="RdBu_r")
ax[2].set(title="v-velocity")

plt.tight_layout()
plt.show()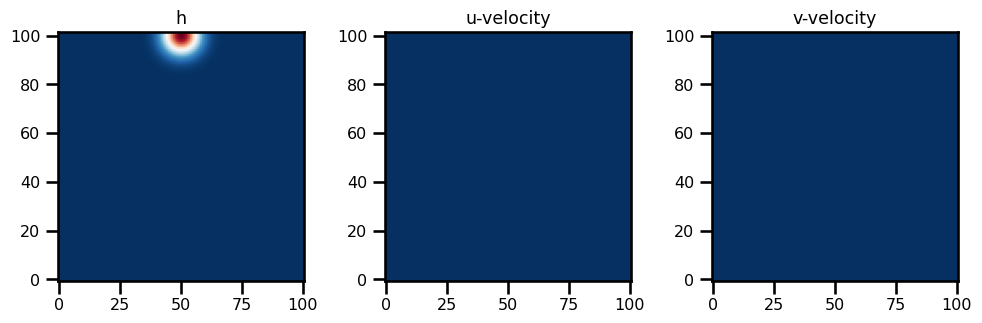

Equation of Motion¶

H RHS¶

Looking at equation (1), we can look at just the height, $h$ , field. This is given by:

\begin{aligned} \frac{\partial h}{\partial t} &+ H \left(\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \right) = 0 \end{aligned}

(2)

Let's write a dedicated function explicitly using this.

LinearShallowWater2D.equation_of_motion_h??

Signature:
LinearShallowWater2D.equation_of_motion_h(
    state: jaxsw._src.models.sw.State,
    params: jaxsw._src.models.sw.Params,
) -> jax.Array
Source:   
    @staticmethod
    def equation_of_motion_h(state: State, params: Params) -> Array:
        """
        Equation:
             ∂h/∂t + H (∂u/∂x + ∂v/∂y) = 0
        """
        # parse state container
        h, u, v = state.h, state.u, state.v

        # parse params container
        depth, domain = params.depth, params.domain

        # create empty matrix
        h_rhs = jnp.zeros_like(h)

        # create RHS
        du_dx = fdx.difference(
            u, axis=0, accuracy=1, method="backward", step_size=domain.dx[0]
        )
        dv_dy = fdx.difference(
            v, axis=1, accuracy=1, method="backward", step_size=domain.dx[1]
        )

        # set the interior points only
        h_rhs = h_rhs.at[1:-1, 1:-1].set(
            -depth * (du_dx[1:-1, 1:-1] + dv_dy[1:-1, 1:-1])
        )
        return h_rhs
File:      ~/code_projects/jaxsw/jaxsw/_src/models/sw/linear.py
Type:      function

h_rhs = LinearShallowWater2D.equation_of_motion_h(state_init, params)

plt.imshow(h_rhs, origin="lower", cmap="RdBu_r")

<matplotlib.image.AxesImage at 0x17e2ac4f0>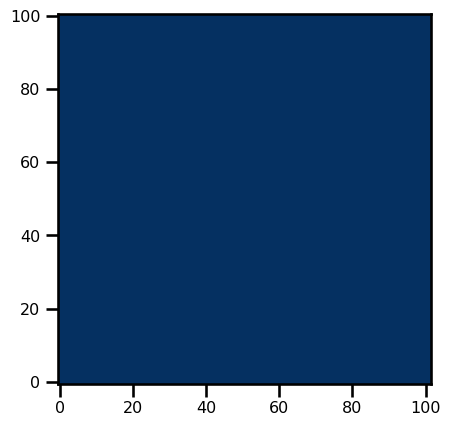

U-Velocity¶

LinearShallowWater2D.equation_of_motion_u??

Signature:
LinearShallowWater2D.equation_of_motion_u(
    state: jaxsw._src.models.sw.State,
    params: jaxsw._src.models.sw.Params,
) -> jaxsw._src.models.sw.State
Source:   
    @staticmethod
    def equation_of_motion_u(state: State, params: Params) -> State:
        """Equation of Motion for the u-component

        Equation:
            ∂u/∂t = fv - g ∂h/∂x
        """
        # parse state and params
        h, u, v = state.h, state.u, state.v
        gravity, domain = params.gravity, params.domain

        coriolis = params.coriolis_param(domain)

        u_rhs = jnp.zeros_like(u)

        v_avg = F_grid.center_average_2D(v[1:, :-1], padding="valid")
        v_avg *= coriolis[1:-1, 1:-1]

        dh_dx = fdx.difference(
            h, axis=0, accuracy=1, method="forward", step_size=domain.dx[0]
        )
        dh_dx *= -gravity

        u_rhs = u_rhs.at[1:-1, 1:-1].set(v_avg + dh_dx[1:-1, 1:-1])

        return u_rhs
File:      ~/code_projects/jaxsw/jaxsw/_src/models/sw/linear.py
Type:      function

u_rhs = LinearShallowWater2D.equation_of_motion_u(state_init, params)

plt.imshow(u_rhs.T, origin="lower", cmap="RdBu_r")

<matplotlib.image.AxesImage at 0x17e0c1850>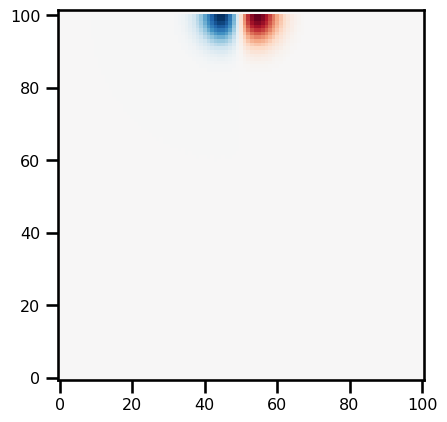

V-Velocity¶

LinearShallowWater2D.equation_of_motion_v??

Signature:
LinearShallowWater2D.equation_of_motion_v(
    state: jaxsw._src.models.sw.State,
    params: jaxsw._src.models.sw.Params,
) -> jax.Array
Source:   
    @staticmethod
    def equation_of_motion_v(state: State, params: Params) -> Array:
        """Equation of motion for v-component
        Equation:
            ∂v/∂t = - fu - g ∂h/∂y
        """
        # parse state and parameters
        h, u, v = state.h, state.u, state.v
        gravity, domain = params.gravity, params.domain

        coriolis = params.coriolis_param(domain)

        v_rhs = jnp.zeros_like(v)

        u_avg = F_grid.center_average_2D(u[:-1, 1:], padding="valid")
        u_avg *= -coriolis[1:-1, 1:-1]

        dh_dy = fdx.difference(
            h, axis=1, accuracy=1, method="forward", step_size=domain.dx[1]
        )
        dh_dy *= -gravity

        v_rhs = v_rhs.at[1:-1, 1:-1].set(u_avg + dh_dy[1:-1, 1:-1])
        return v_rhs
File:      ~/code_projects/jaxsw/jaxsw/_src/models/sw/linear.py
Type:      function

v_rhs = LinearShallowWater2D.equation_of_motion_v(state_init, params)

plt.imshow(v_rhs, origin="lower", cmap="RdBu_r")

<matplotlib.image.AxesImage at 0x17e25a5b0>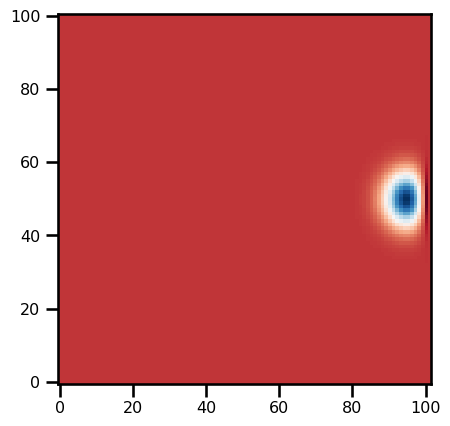

Boundary Conditions¶

# initialize state
state_init = SWMState.init_state(params, init_h0)

# apply boundary conditions
state_init = LinearShallowWater2D.boundary_f(state_init, "h")
state_init = LinearShallowWater2D.boundary_f(state_init, "u")
state_init = LinearShallowWater2D.boundary_f(state_init, "v")

# apply RHS
h_rhs = LinearShallowWater2D.equation_of_motion_h(state_init, params)
v_rhs = LinearShallowWater2D.equation_of_motion_v(state_init, params)
u_rhs = LinearShallowWater2D.equation_of_motion_u(state_init, params)

fig, ax = plt.subplots(ncols=3, figsize=(10, 5))
ax[0].imshow(h_rhs.T, origin="lower", cmap="RdBu_r")
ax[0].set(title="h")

ax[1].imshow(u_rhs.T, origin="lower", cmap="RdBu_r")
ax[1].set(title="u-velocity")

ax[2].imshow(v_rhs.T, origin="lower", cmap="RdBu_r")
ax[2].set(title="v-velocity")

plt.tight_layout()
plt.show()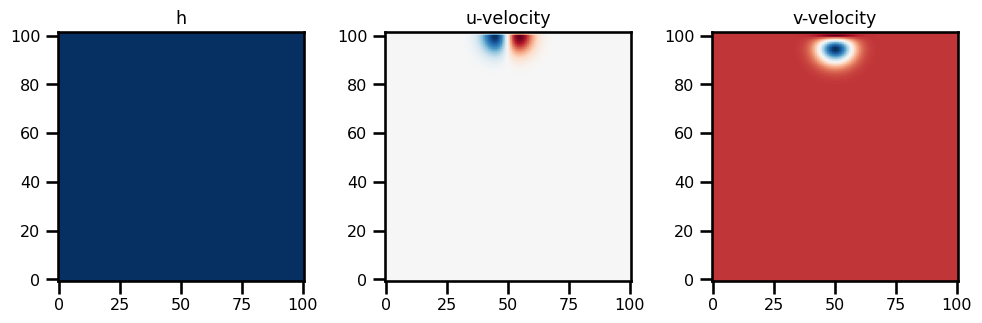

state_update = LinearShallowWater2D.equation_of_motion(0, state_init, params)

fig, ax = plt.subplots(ncols=3, figsize=(10, 5))
ax[0].imshow(h_rhs.T, origin="lower", cmap="RdBu_r")
ax[0].set(title="h")

ax[1].imshow(u_rhs.T, origin="lower", cmap="RdBu_r")
ax[1].set(title="u-velocity")

ax[2].imshow(v_rhs.T, origin="lower", cmap="RdBu_r")
ax[2].set(title="v-velocity")

plt.tight_layout()
plt.show()

Time Stepping¶

# TEMPORAL DISCRETIZATION
# initialize temporal domain

dt = 0.25 * domain.dx[0] / np.sqrt(params.gravity * params.depth)
print(f"Step Size (dt): {dt:.4e}")

tmin = 0.0
tmax = pd.to_timedelta(2.0, unit="days").total_seconds()
num_save = 100

Step Size (dt): 1.5964e+02

import pandas as pd

t_domain = TimeDomain(tmin=tmin, tmax=tmax, dt=dt)
ts = jnp.linspace(tmin, tmax, num_save)
saveat = dfx.SaveAt(ts=ts)

# DYNAMICAL SYSTEM
dyn_model = LinearShallowWater2D(t_domain=t_domain, saveat=saveat)

Integration¶

# Euler, Constant StepSize
solver = dfx.Tsit5()

# Tolerances
stepsize_controller = dfx.ConstantStepSize()
# rtol = 1e-3
# atol = 1e-4
# stepsize_controller = dfx.PIDController(
#     pcoeff=0.3, icoeff=0.4, rtol=rtol, atol=atol, dtmax=dt
# )

# SPATIAL DISCRETIZATION
params_init = SWMParams(
    depth=100.0, gravity=9.81, coriolis_f0=2e-4, coriolis_beta=2e-11, domain=domain
)
state_init = SWMState.init_state(params_init, init_h0)


# integration
sol = dfx.diffeqsolve(
    terms=dfx.ODETerm(dyn_model.equation_of_motion),
    solver=solver,
    t0=ts.min(),
    t1=ts.max(),
    dt0=dt,
    y0=state_init,
    saveat=saveat,
    args=params_init,
    stepsize_controller=stepsize_controller,
    max_steps=None,
)

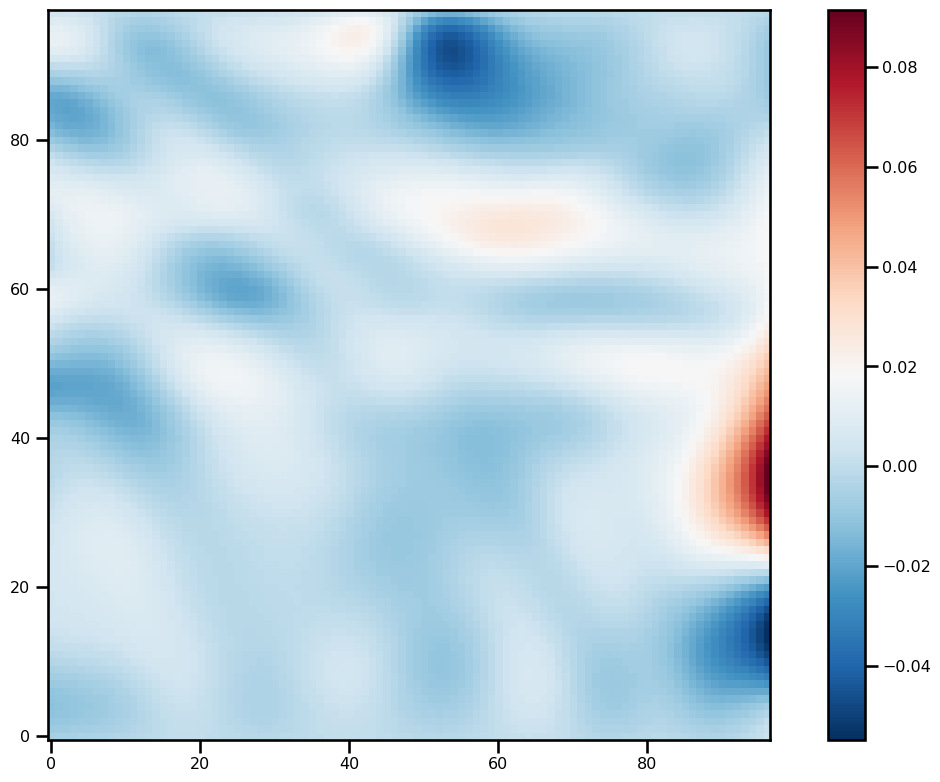
for ivar in sol.ys:
    fig, ax = plt.subplots(figsize=(12, 8))
    pts = ax.imshow(ivar[-1][2:-2, 2:-2].T, origin="lower", cmap="RdBu_r")
    plt.colorbar(pts)
    plt.tight_layout()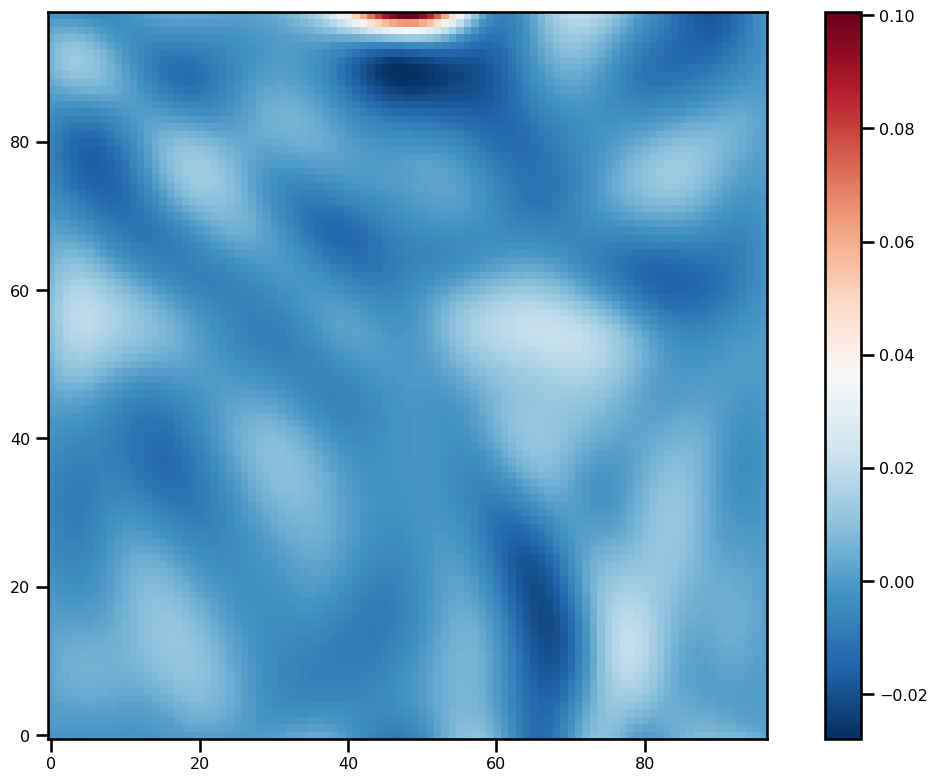

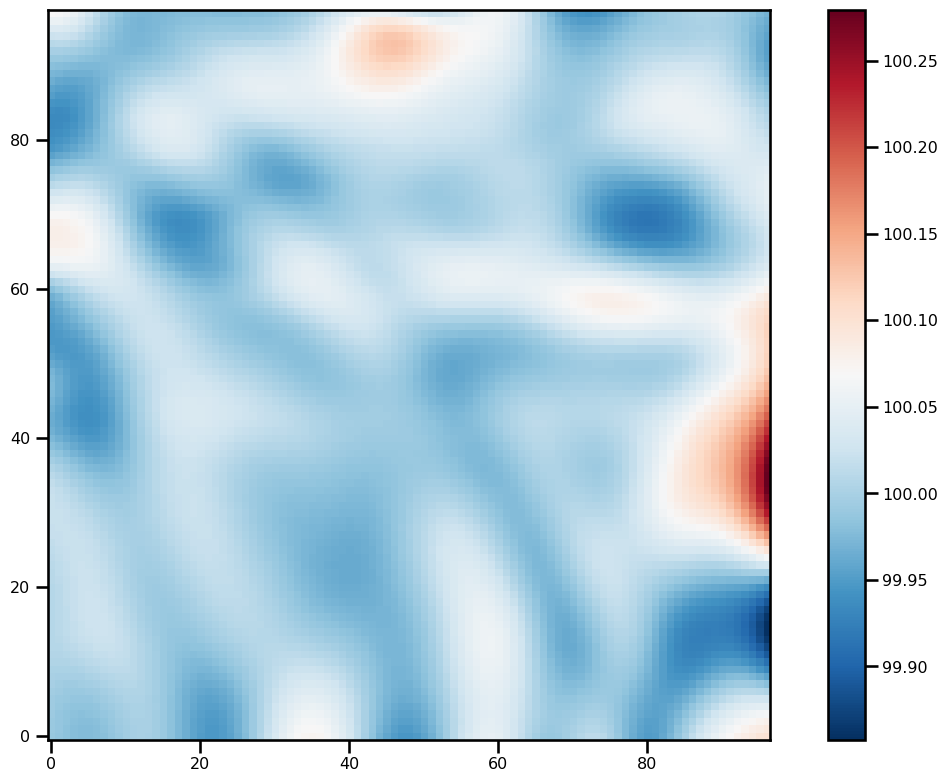
Analysis¶

ds_results = xr.Dataset(
    data_vars={
        "u": (("time", "x", "y"), sol.ys.u),
        "v": (("time", "x", "y"), sol.ys.v),
        "h": (("time", "x", "y"), sol.ys.h),
    },
    coords={
        "time": (("time"), sol.ts),
        "x": (("x"), domain.coords[0]),
        "y": (("y"), domain.coords[1]),
    },
)
ds_results

ds_results.to_netcdf("./sw_linear_rossby.nc")

from xmovie import Movie
from pathlib import Path
from matplotlib import ticker


from xmovie import Movie
from pathlib import Path
from matplotlib import ticker


def custom_plot_h_ke_layers(ds, fig, tt, *args, **kwargs):
    sub = ds.isel(time=tt)
    time = sub.v.time.values / 86400

    xlim = kwargs.pop("xlim", None)
    ylim = kwargs.pop("ylim", None)
    vmin_h = kwargs.pop("vmin_h", sub.h.isel(x=slice(1, -1), y=slice(1, -1)).min())
    vmax_h = kwargs.pop("vmax_h", sub.h.isel(x=slice(1, -1), y=slice(1, -1)).max())
    cmap = kwargs.pop("cmap", "viridis")

    fig.set_size_inches(12, 4.5)

    ax = fig.subplots(
        ncols=2,
    )

    # HEIGHT
    cbar_kwargs = {"label": "Height [m]"}
    pts = sub.h.isel(x=slice(1, -1), y=slice(1, -1)).plot.pcolormesh(
        ax=ax[0],
        cmap="viridis",
        add_colorbar=True,
        vmin=vmin_h,
        vmax=vmax_h,
        cbar_kwargs=cbar_kwargs,
        # **kwargs
    )
    loc = ticker.MaxNLocator(6)
    levels = loc.tick_values(vmin_h, vmax_h)
    sub.h.isel(x=slice(1, -1), y=slice(1, -1)).plot.contour(
        ax=ax[0],
        levels=levels,
        vmin=vmin_h,
        vmax=vmax_h,
        alpha=0.5,
        linewidths=1,
        cmap="black",
        linestyles=np.where(levels >= 0, "-", "--"),
    )

    # ax.set_aspect('equal')
    pts = ax[0].set(xlabel="x [m]", ylabel="y [m]", title=f"Time: {time:.4f} day(s)")

    # U-VELOCITY
    cbar_kwargs = {"label": "√ Kinetic Energy [ms$^{-2}$]"}
    vmin_ke = kwargs.pop("vmin_ke", sub.ke.isel(x=slice(1, -1), y=slice(1, -1)).min())
    vmax_ke = kwargs.pop("vmax_ke", sub.ke.isel(x=slice(1, -1), y=slice(1, -1)).max())
    pts = sub.ke.isel(x=slice(1, -2), y=slice(1, -2)).plot.pcolormesh(
        ax=ax[1],
        cmap="YlGnBu_r",
        add_colorbar=True,
        vmin=vmin_ke,
        vmax=vmax_ke,
        cbar_kwargs=cbar_kwargs
        # **kwargs
    )
    loc = ticker.MaxNLocator(6)
    levels = loc.tick_values(vmin_ke, vmax_ke)
    sub.ke.isel(x=slice(1, -2), y=slice(1, -2)).plot.contour(
        ax=ax[1],
        levels=levels,
        vmin=vmin_ke,
        vmax=vmax_ke,
        alpha=0.5,
        linewidths=1,
        cmap="black",
        linestyles=np.where(levels >= 0, "-", "--"),
    )

    # ax.set_aspect('equal')
    pts = ax[1].set(xlabel="x [m]", ylabel="y [m]", title=f"Time: {time:.4f} day(s)")

    plt.tight_layout()
    return None, None


from pathlib import Path


def create_movie(
    var,
    name,
    plotfunc=custom_plot_h_ke_layers,
    framedim: str = "steps",
    file_path=None,
    **kwargs,
):
    if file_path is not None:
        file_name = Path(file_path).joinpath(f"movie_{name}.gif")
    else:
        file_name = Path(f"./movie_{name}.gif")

    mov = Movie(
        var, plotfunc=plotfunc, framedim=framedim, **kwargs, dpi=200, input_check=False
    )
    mov.save(
        file_name,
        remove_movie=False,
        progress=True,
        framerate=3,
        gif_framerate=3,
        overwrite_existing=True,
        gif_resolution_factor=0.5,
        parallel=False,
    )

    return None

%matplotlib inline
vmin_h = ds_results.h.isel(x=slice(2, -2), y=slice(2, -2)).min()
vmax_h = ds_results.h.isel(x=slice(2, -2), y=slice(2, -2)).max()

ds_results["ke"] = np.sqrt(0.5 * (ds_results.u**2 + ds_results.v**2))

vmin_ke = ds_results.ke.isel(x=slice(2, -2), y=slice(2, -2)).min()
vmax_ke = ds_results.ke.isel(x=slice(2, -2), y=slice(2, -2)).max()

mov = Movie(
    ds_results.transpose("time", "y", "x"),
    plotfunc=custom_plot_h_ke_layers,
    framedim="time",
    input_check=False,
    vmin_h=vmin_h,
    vmax_h=vmax_h,
    vmin_ke=vmin_ke,
    vmax_ke=vmax_ke,
)
mov.preview(60)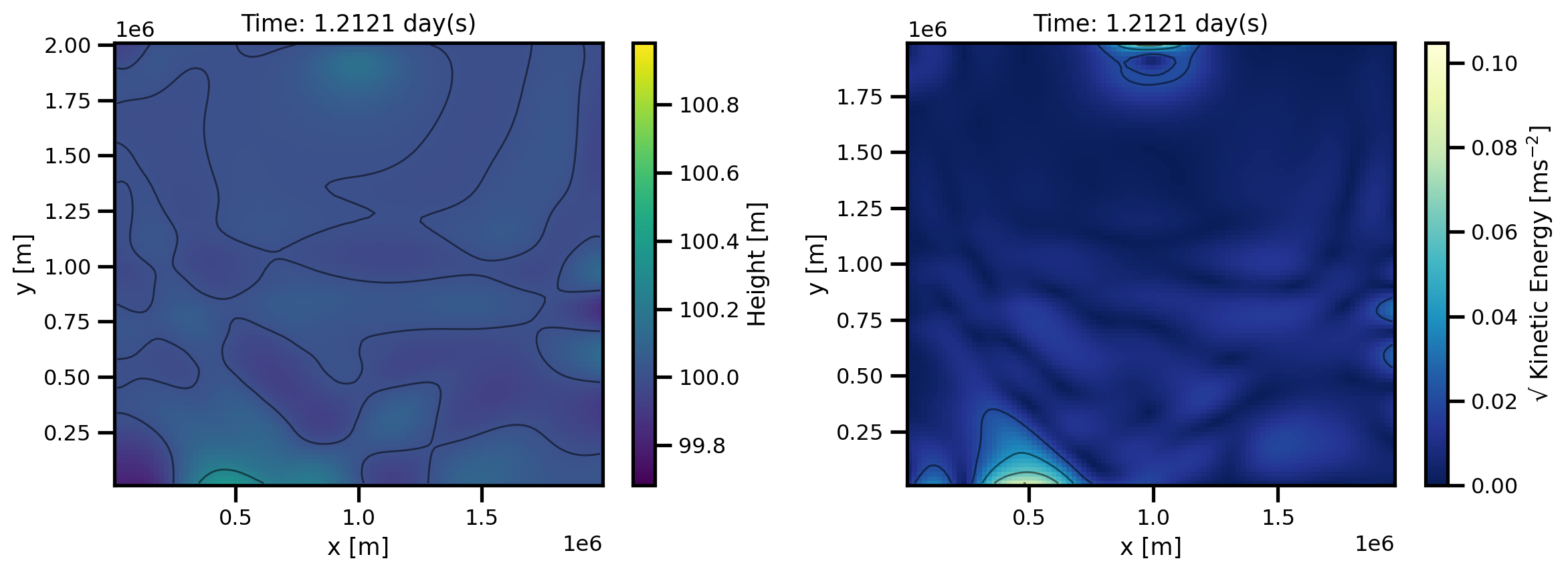

create_movie(
    ds_results.transpose(
        "time", "y", "x"
    ),  # .sel(time=slice("2017-02-01", "2017-03-01")),
    name="swe_linear_rossby",
    plotfunc=custom_plot_h_ke_layers,
    file_path="./",
    framedim="time",
    cmap="viridis",
    robust=True,
    vmin_h=vmin_h,
    vmax_h=vmax_h,
    vmin_ke=vmin_ke,
    vmax_ke=vmax_ke,
)