Lorenz 63

J. Emmanuel JohnsonTakaya Uchida

import autoroot  # noqa: F401, I001
import jax
import jax.numpy as jnp
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import diffrax as dfx
import xarray as xr
import equinox as eqx

from jaxsw import L63State, Lorenz63, rhs_lorenz_63

sns.reset_defaults()
sns.set_context(context="talk", font_scale=0.7)

%matplotlib inline
%load_ext autoreload
%autoreload 2

Lorenz 63¶

Equation of Motion
Observation Operator
Integrate

Equation of Motion¶

\begin{aligned} \frac{dx}{dt} &= \sigma (y - x) \\ \frac{dy}{dt} &= x (\rho - z) - y \\ \frac{dz}{dt} &= xy - \beta z \end{aligned}

(1)

where $(\sigma,\rho,\beta)$ are hyperparameters.

# initialize state
state = L63State.init_state(noise=0.01)

x, y, z = state.x, state.y, state.z
print(x.shape, y.shape, z.shape, state.array.shape)

(1,) (1,) (1,) (3,)

sigma, rho, beta = 10, 28, 2.667

# initialize state and params
state, params = L63State.init_state_and_params(noise=0.01, sigma=10, rho=28, beta=2.667)

# rhs
x, y, z = state.x, state.y, state.z
sigma, rho, beta = params.sigma, params.rho, params.beta

state_dot = rhs_lorenz_63(x=x, y=y, z=z, sigma=sigma, rho=rho, beta=beta)

x_dot, y_dot, z_dot = state_dot

assert x.shape == y.shape == z.shape == x_dot.shape
assert x_dot.shape == y_dot.shape == z_dot.shape == x.shape

Model¶

# initialize state
state_init, params = L63State.init_state_and_params(
    noise=0.01, sigma=10, rho=28, beta=2.667
)

# initialize model
l63_model = Lorenz63()

# step through
state_dot = l63_model.equation_of_motion(t=0, state=state_init, args=params)

state_dot

L63State(x=Array([0.07530808], dtype=float32), y=Array([25.796669], dtype=float32), z=Array([-1.6745309], dtype=float32))

Time Stepping¶

dt = 0.01
t0 = 0.0
t1 = 30.0
# observe_every = 10
ts = jnp.arange(t0, t1, dt)
num_tsteps = len(ts)

saveat = dfx.SaveAt(t0=t0, t1=t1, ts=ts)
saveat

SaveAt(
  subs=SubSaveAt(
    t0=0.0,
    t1=30.0,
    ts=f32[3000],
    steps=False,
    fn=<function save_y>
  ),
  dense=False,
  solver_state=False,
  controller_state=False,
  made_jump=False
)

# Euler, Constant StepSize
solver = dfx.Euler()
stepsize_controller = dfx.ConstantStepSize()

# integration
sol = dfx.diffeqsolve(
    terms=dfx.ODETerm(l63_model.equation_of_motion),
    solver=solver,
    t0=ts.min(),
    t1=ts.max(),
    dt0=dt,
    y0=state_init,
    saveat=saveat,
    args=params,
    stepsize_controller=stepsize_controller,
)

sol.ys.x.shape, sol.ts.shape

((3001, 1), (3001,))

ds_sol = xr.Dataset(
    {
        "x": (("time"), sol.ys.x.squeeze()),
        "y": (("time"), sol.ys.y.squeeze()),
        "z": (("time"), sol.ys.z.squeeze()),
    },
    coords={
        "time": (["time"], np.asarray(sol.ts)),
    },
    attrs={
        "ode": "lorenz_63",
        "sigma": params.sigma,
        "beta": params.beta,
        "rho": params.rho,
    },
)

ds_sol

fig, ax = plt.subplots(figsize=(5, 4))

ds_sol.x.plot(ax=ax, label="x")
ds_sol.y.plot(ax=ax, label="y")
ds_sol.z.plot(ax=ax, label="z")

ax.set_xlabel("Time")
ax.set_ylabel("Values")
ax.set_title("Trajectory")

plt.legend()
plt.tight_layout()
plt.show()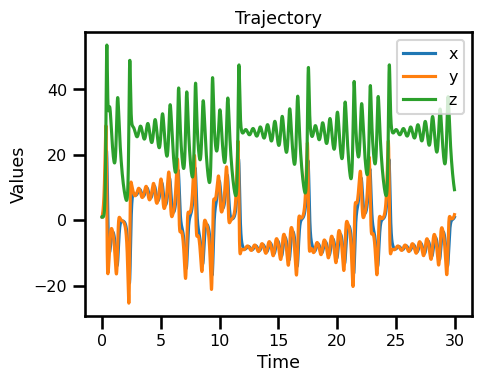

fig, ax = plt.subplots(subplot_kw={"projection": "3d"})

ax.plot(
    ds_sol.x,
    ds_sol.y,
    ds_sol.z,
    lw=1.0,
    color="blue",
    label="Trajectory",
)
# ax.scatter3D(out.x[::10], out.y[::10], out.z[::10], lw=0.5, color="red", label="y")

ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
plt.legend()
plt.tight_layout()
plt.show()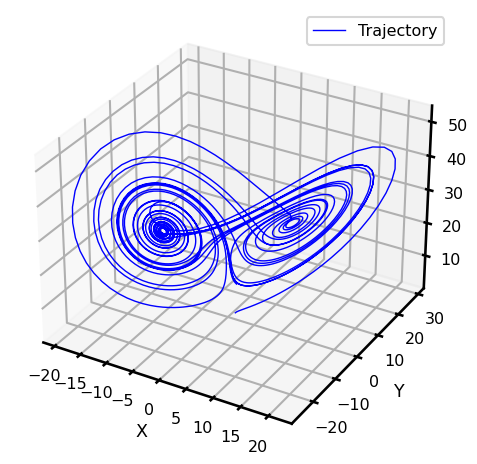

Generating Observations¶

ds_sol_ = ds_sol.to_array(dim="component", name="simulation").to_dataset()
ds_sol_

ds_sol = ds_sol.to_array(dim="component", name="simulation").to_dataset()

ds_sol["observations"] = xr.full_like(ds_sol.simulation, np.nan)

ds_sol

Missing Time¶

sample_step = 20
ds_sol["observations"] = xr.full_like(ds_sol.simulation, np.nan)
ds_sol["observations"].loc[::sample_step] = ds_sol["simulation"].loc[::sample_step]

fig, ax = plt.subplots(subplot_kw={"projection": "3d"})

ax.plot(
    ds_sol.simulation.sel(component="x"),
    ds_sol.simulation.sel(component="y"),
    ds_sol.simulation.sel(component="z"),
    lw=1.0,
    color="blue",
    label="Trajectory",
)
ax.scatter3D(
    ds_sol.observations.sel(component="x"),
    ds_sol.observations.sel(component="y"),
    ds_sol.observations.sel(component="z"),
    lw=0.5,
    color="red",
    label="Observations",
)

ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
plt.legend()
plt.tight_layout()
plt.show()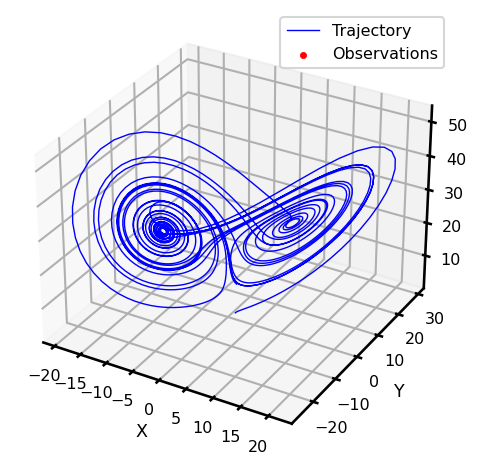

Adding Noise¶

# def add_noise(da, sigma=2**.5):
#     return da  + np.random.randn(*da.shape) * sigma

sigma = 2**0.5

ds_sol["observations"] += sigma * np.random.randn(*ds_sol["observations"].shape)

fig, ax = plt.subplots(subplot_kw={"projection": "3d"})

ax.plot(
    ds_sol.simulation.sel(component="x"),
    ds_sol.simulation.sel(component="y"),
    ds_sol.simulation.sel(component="z"),
    lw=1.0,
    color="blue",
    label="Trajectory",
)
ax.scatter3D(
    ds_sol.observations.sel(component="x"),
    ds_sol.observations.sel(component="y"),
    ds_sol.observations.sel(component="z"),
    lw=0.5,
    color="red",
    label="Observations",
)

ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")
plt.legend()
plt.tight_layout()
plt.show()

Batch of Observations¶

# initialize state
state = L63State.init_state(noise=0.01, batchsize=100)

x, y, z = state.x, state.y, state.z
print(x.shape, y.shape, z.shape, state.array.shape)

# initialize model
l63_model = Lorenz63()

(100, 1) (100, 1) (100, 1) (100, 3)

batchsize = 100
sigma, rho, beta = 10, 28, 2.667

state_batch, params = L63State.init_state_and_params(
    batchsize=batchsize, noise=0.01, sigma=10, rho=28, beta=2.667
)

fn_batched = jax.vmap(rhs_lorenz_63, in_axes=(0, 0, 0, None, None, None))

state_dot_batch = fn_batched(
    state_batch.x, state_batch.y, state_batch.z, sigma, rho, beta
)
x_dot, y_dot, z_dot = state_dot_batch
# state_dot_batch = fn_batched(state_batch)

assert x_dot.shape == y_dot.shape == z_dot.shape == state_batch.x.shape
assert state_batch.x.shape == state_batch.y.shape == state_batch.z.shape == x_dot.shape


fn_batched = jax.vmap(l63_model.equation_of_motion, in_axes=(None, 0, None))

state_dot_batch_ = fn_batched(0, state_batch, params)
x_dot_, y_dot_, z_dot_ = state_dot_batch_
# state_dot_batch = fn_batched(state_batch)

np.testing.assert_array_equal(x_dot, x_dot_)
np.testing.assert_array_equal(y_dot, y_dot_)
np.testing.assert_array_equal(z_dot, z_dot_)
assert x_dot.shape == y_dot.shape == z_dot.shape == state_batch.x.shape
assert state_batch.x.shape == state_batch.y.shape == state_batch.z.shape == x_dot.shape

dt = 0.01
t0 = 0.0
t1 = 30.0
# observe_every = 10
ts = jnp.arange(t0, t1, dt)
num_tsteps = len(ts)

saveat = dfx.SaveAt(t0=t0, t1=t1, ts=ts)
saveat

SaveAt(
  subs=SubSaveAt(
    t0=0.0,
    t1=30.0,
    ts=f32[3000],
    steps=False,
    fn=<function save_y>
  ),
  dense=False,
  solver_state=False,
  controller_state=False,
  made_jump=False
)

# Euler, Constant StepSize
solver = dfx.Euler()
stepsize_controller = dfx.ConstantStepSize()

# integration
integrate = lambda state: dfx.diffeqsolve(
    terms=dfx.ODETerm(l63_model.equation_of_motion),
    solver=solver,
    t0=t0,
    t1=t1,
    dt0=dt,
    y0=state,
    saveat=saveat,
    args=params,
    stepsize_controller=stepsize_controller,
)
sol = jax.vmap(integrate)(state_batch)

state_batch.x.shape, sol.ys.x.shape

((100, 1), (100, 3001, 1))

ds_sol = xr.Dataset(
    {
        "x": (("realization", "time"), sol.ys.x.squeeze()),
        "y": (("realization", "time"), sol.ys.y.squeeze()),
        "z": (("realization", "time"), sol.ys.z.squeeze()),
    },
    coords={
        "time": (["time"], sol.ts[0].squeeze()),
    },
    attrs={
        "ode": "lorenz_63",
        "sigma": params.sigma,
        "beta": params.beta,
        "rho": params.rho,
    },
)

ds_sol

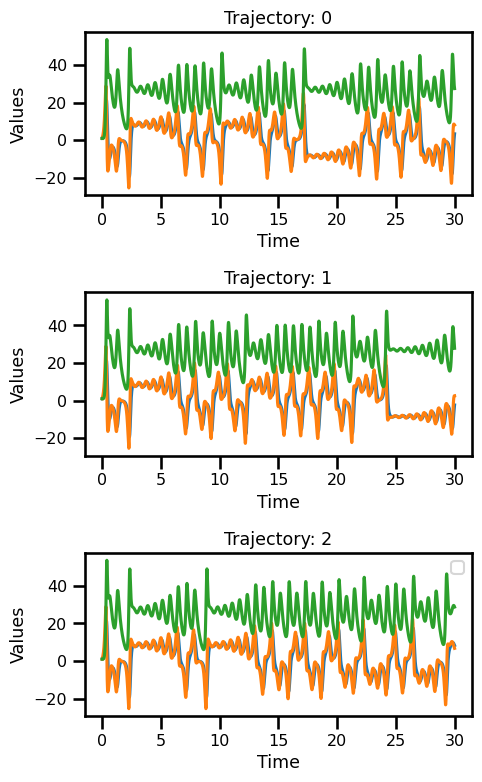
fig, ax = plt.subplots(nrows=3, figsize=(5, 8))

for i in range(3):
    ds_sol.x.sel(realization=i).plot(ax=ax[i])
    ds_sol.y.sel(realization=i).plot(ax=ax[i])
    ds_sol.z.sel(realization=i).plot(ax=ax[i])

    ax[i].set_xlabel("Time")
    ax[i].set_ylabel("Values")
    ax[i].set_title(f"Trajectory: {i}")


plt.legend()
plt.tight_layout()
plt.show()

No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.