Jensens Inequality#
This theorem is one of those sleeper theorems which comes up in a big way in many machine learning problems.
The Jensen inequality theorem states that for a convex function \(f\),
A convex function (or concave up) is when there exists a minimum to that function. If we take two points on any part of the graph and draw a line between them, we will be above or at (as a limit) the minimum point of the graph. We can flip the signs for a concave function. But we want the convex property because then it means it has a minimum value and this is useful for minimization strategies. Recall from Calculus class 101: let’s look at the function \(f(x)=\log x\).
We can use the second derivative test to find out if a function is convex or not. If \(f'(x) \geq 0\) then it is concave up (or convex). I’ll map out the derivatives below:
You’ll see that \(-\frac{1}{x^2}\leq 0\) for \(x \in [0, \infty)\). This means that \(\log x\) is a concave function. So, the solution to this if we want a convex function is to take the negative \(\log\) (which adds intuition as to why we typically take the negative log likelihood of many functions).
Variational Inference#
Typically in the VI literature, they add this Jensen inequality property in order to come up with the Evidence Lower Bound (ELBO). But I never understood how it worked because I didn’t know if they wanted the convex or concave. If we think of the loss function of the likelihood \(\mathcal{L}(\theta)\) and the ELBO \(\mathcal{F}(q, \theta)\). Take a look at the figure from
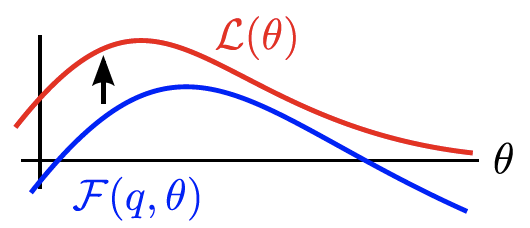
Fig. 1 A quick demo with the Elbo inequality.#
Typically we use the \(\log\) function when it’s used
Resources
MIT OpenCourseWare - Intro Prob. | Inequalitiese, Convergence and Weak Law of Large Numbers
