Deep Markov Model#

Notes for the Deep Markov Model (DMM) algorithm.

\[\begin{split} \begin{aligned} z_0 &= \mathcal{N}(z_0|\mu_0, \Sigma_0)\\ p(z_t|z_{t-1}) &= \mathcal{N}(z_t|\boldsymbol{\mu}_{\text{trans}}(z_{t-1}), \boldsymbol{\sigma}^2_{\text{trans}}(z_{t_1})) \\ p(x_t|z_t) &= \mathcal{N}(x_t|\boldsymbol{\mu}_{\text{emiss}}(z_t), \boldsymbol{\sigma}^2_{\text{emiss}}(z_t)) \\ \end{aligned} \end{split}\]

Notes on Deep Markov Models (DMM) (aka Deep Kalman Filters (DKF))

State Space Model#

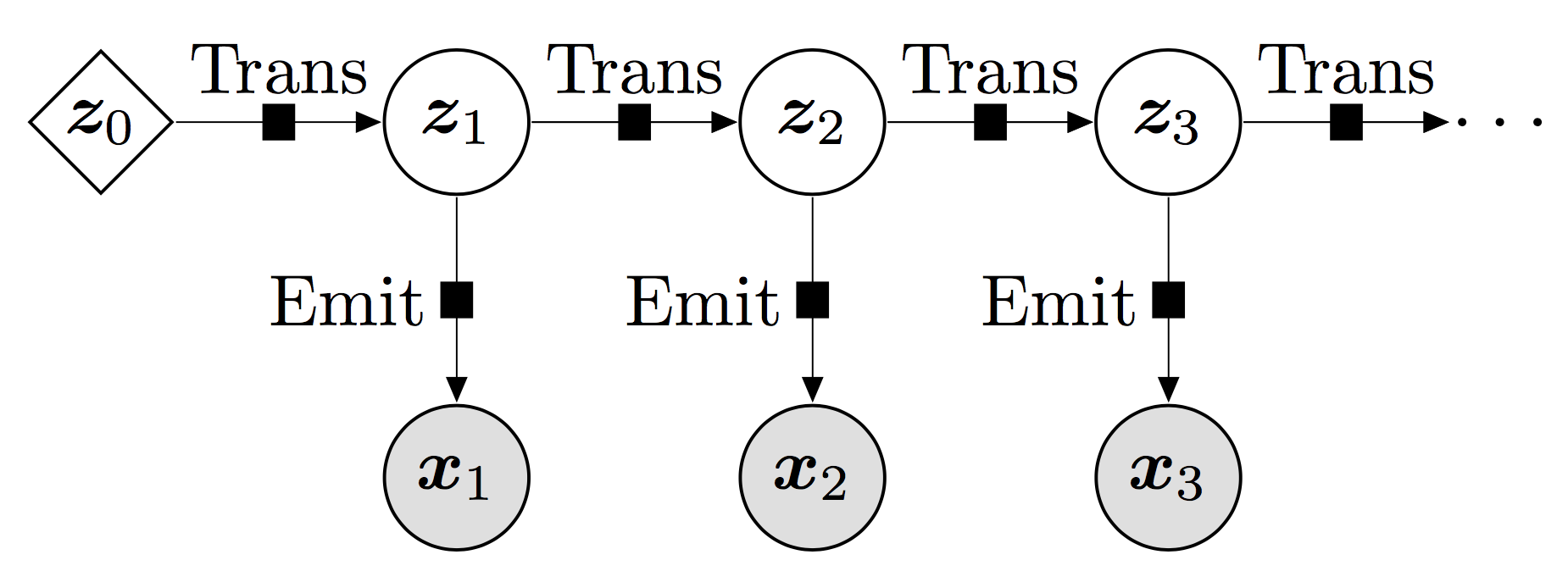
../../../_images/dmm_graph.png

Fig. 9 This showcases the interaction between the hidden state and the observations wrt time. The most important property is the Markovian property which dictates that the future state only depends upon the current state and no other previous states obtained before. Source: pyro Deep Markov Model Tutorial.#

We are taking the same state-space model as before. However, this time, we do not restrict ourselves to linear functions. We allow for non-linear functions for the transition and emission functions.

We allow for a non-linear function, \(\boldsymbol f\), for the transition model between states.

(59)#\[ \mathbf{z}_t = \boldsymbol{f}(\mathbf{z}_{t-1}; \boldsymbol{\theta}_t) + \boldsymbol{\delta}_t \]

We also put a non-linear function, \(\boldsymbol h\), for the emission model to describe the relationship between the state and the measurements. $\( \mathbf{x}_t = \boldsymbol{h}(\mathbf{z}_t; \boldsymbol{\theta}_e) + \boldsymbol{\epsilon}_t \)$(dmm_emission)

We are still going to assume that the output is Gaussian distributed (in the case of regression, otherwise this can be a Bernoulli distribution). We can write these distributions as follows:

\[\begin{split} \begin{aligned} p_{\theta_t}(\mathbf{z}_t|\mathbf{z}_{t-1}) &= \mathcal{N}(\mathbf{z}_t; \boldsymbol{f}(\mathbf{z}_{t-1}; \boldsymbol{\theta}_t),\mathbf{Q}_t) \\ p(\mathbf{x}_t|\mathbf{z}_t) &= \mathcal{N}(\mathbf{x}_t; \boldsymbol{h}(\mathbf{z}_t; \boldsymbol{\theta}_e), \mathbf{R}_t) \end{aligned} \end{split}\]

where \(\theta_t\) is the parameterization for the transition model and \(\theta_e\) is the parameterization for the emission model. Notice how this assumes some non-linear transformation on the means of the Gaussian distributions however, we still want the output to be Gaussian.

If we are given all of the observations, \(\mathbf{x}_{1:T}\), we can write the joint distribution as:

\[ p(\mathbf{x}_{1:T}, \mathbf{z}_{1:T}) = p(\mathbf{x}_{1:T}|\mathbf{z}_{1:T})p(\mathbf{z}_{1:T}) \]

If we wish to find the best function parameters based on the data, we can still calculate the marginal likelihood by integrating out the state, \(\mathbf{z}_{1:T}\):

(60)#\[ p_{\boldsymbol \theta}(\mathbf{x}_{1:T}) = \int p_{\theta_e}(\mathbf{x}_{1:T}|\mathbf{z}_{1:T})p_{\theta_e}(\mathbf{z}_{1:T})d\mathbf{z}_{1:T} \]

Inference#

We can learn the parameters, \(\boldsymbol \theta\), of the prescribed model by minimizing the marginal log-likelihood. We can log transform the marginal likelihood function (eq (60)).

\[ \log p_{\boldsymbol \theta}(\mathbf{x}) = \mathbb{E}_{\mathbf{z} \sim p_{\boldsymbol \theta}(\mathbf{z}|\mathbf{x})} \left[ \log p_{\theta_e}(\mathbf{x}|\mathbf{z}) + \log p_{\theta_e}(\mathbf{z})\right] \]

Loss Function#

(61)#\[ \mathcal{L}(\boldsymbol{\theta},\boldsymbol{\phi}; \mathbf{x}) = \sum_{t=1}^T \mathbb{E}_{q_{\boldsymbol \phi}}\left[ \log \underbrace{p_{\boldsymbol{\theta}_t}(\mathbf{z}_t|\mathbf{z}_{t-1})}_{\text{Transition}} + \log \underbrace{p_{\boldsymbol{\theta}_e}(\mathbf{x}_t|\mathbf{z}_{t})}_{\text{Emission}} - \log \underbrace{q_{\boldsymbol{\phi}}(\mathbf{z}_t|\mathbf{z}_{t-1}, \mathbf{x}_{1:T})}_{\text{Inference}} \right] \]

Training#

We can estimate the gradients

Literature#

Model Components#

Transition Function#

\[ p(z_t|z_{t-1}) = \mathcal{N}(z_t|\boldsymbol{\mu}(z_{t-1}), \boldsymbol{\sigma}^2(z_{t_1})) \]

where:

Functions#

Gate

gate = Sequential(
    Linear(latent_dim, hidden_dim),
    ReLU(),
    Linear(hidden_dim, latent_dim),
    Sigmoid(),
)

Proposed Mean

proposed_mean = Sequential(
    Linear(latent_dim, hidden_dim),
    ReLU(),
    Linear(hidden_dim, latent_dim)
)

Mean

z_to_mu = Linear(latent_dim, latent_dim)

LogVar

z_to_logvar = Linear(latent_dim, latent_dim)

Initialization

Here, we want to ensure that the output starts out as the identity function. This helps training so that we don’t start out with completely nonsensical results which can lead to crazy gradients.

z_to_mu.weight = eye(latent_dim)
z_to_mu.bias = eye(latent_dim)

Function

z_gate = gate(z_t_1)
z_prop_mean = proposed_mean(z_t_1)
# mean prediction
z_mu = (1 - z_gate) * z_to_mu(z_t_1) + z_gate * z_prop_mean
# log var predictions
z_logvar = z_to_logvar(nonlin_fn(z_prop_mean))

Emission Function#

\[ p(x_t|z_t) = \mathcal{N}(x_t|\boldsymbol{\mu}_{\text{emiss}}(z_t), \boldsymbol{\sigma}^2_{\text{emiss}}(z_t)) \]

where:

Tabular#

Gate

class Emission:
    def __init__(self, latent_dim, hidden_dim, input_dim) -> None:
        super().__init__()
        self.input_dim = input_dim
        self.z_to_mu = Sequential(
            Linear(latent_dim, hidden_dim),
            Linear(hidden_dim, hidden_dim),
            Linear(hidden_dim, input_dim)
        )
        self.hidden_to_hidden = Linear(hidden_dim)

Proposed Mean

proposed_mean = Sequential(
    Linear(latent_dim, hidden_dim),
    ReLU(),
    Linear(hidden_dim, latent_dim)
)

Mean

z_to_mu = Linear(latent_dim, latent_dim)

LogVar

z_to_logvar = Linear(latent_dim, latent_dim)

Initialization

Here, we want to ensure that the output starts out as the identity function. This helps training so that we don’t start out with completely nonsensical results which can lead to crazy gradients.

z_to_mu.weight = eye(latent_dim)
z_to_mu.bias = eye(latent_dim)

Function

z_gate = gate(z_t_1)
z_prop_mean = proposed_mean(z_t_1)
# mean prediction
z_mu = (1 - z_gate) * z_to_mu(z_t_1) + z_gate * z_prop_mean
# log var predictions
z_logvar = z_to_logvar(nonlin_fn(z_prop_mean))

Resources#

Code#