Entropy Estimator - Histogram#
import sys, os
from pyprojroot import here
# spyder up to find the root
pysim_root = "/home/emmanuel/code/pysim"
# append to path
sys.path.append(str(pysim_root))
import numpy as np
import jax
import jax.numpy as jnp
# MATPLOTLIB Settings
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
# SEABORN SETTINGS
import seaborn as sns
import corner
sns.set_context(context="talk", font_scale=0.7)
%load_ext autoreload
%autoreload 2
# %load_ext lab_black
Demo Data - Gaussian#
from pysim.data.information.studentt import generate_studentt_data
from pysim.data.information.gaussian import generate_gaussian_data
# parameters
n_samples = 1_000
n_features = 1
df = 10
# create seed (trial number)
# res_tuple = generate_studentt_data(n_samples=n_samples, n_features=n_features, df=df)
res_tuple = generate_gaussian_data(n_samples=n_samples, n_features=n_features)
H_true = res_tuple.H
print(f"True Estimator: {H_true:.4f} nats")
True Estimator: 1.5448 nats
fig = corner.corner(res_tuple.X, bins=50)
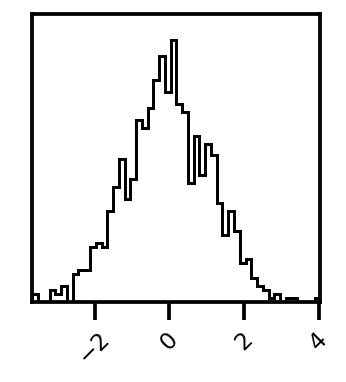
Histogram#
# import numpy as np
# from scipy.stats import rv_histogram
# # histogram parameters
# nbins = "auto"
# data = res_tuple.X.copy()
# data_marginal = data[:, 0]
# # get histogram
# histogram = np.histogram(data_marginal, bins=nbins)
# # create histogram random variable
# hist_dist = rv_histogram(histogram)
Many times we call for an empirical estimator:
where \(\hat{p}_k=\frac{h_k}{n}\) are the maximum likelihood estimates of each probability \(p_k\) and \(h_k=\sum_{i}^n\boldsymbol{1}_{\{X_i=k\}}\)
Resources:
Antos & Kontoyiannis (2001) - “plug-in” estimator
Strong et. al. (1998) - “naive” estimator
Fortunately, the scipy method already does this for us.
From Scratch#
1. Histogram#
# histogram parameters
nbins = "auto"
data = res_tuple.X.copy()
# get hist counts and bin edges
data_min = data.min() #- 0.1
data_max = data.max() #+ 0.1
n_samples = data.shape[0]
bins = int(jnp.sqrt(n_samples))
counts, bin_edges = jnp.histogram(data, bins=bins, range=(data_min, data_max), density=False)
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
Note:
It’s always good practice to leave a bit of room for the boundaries.
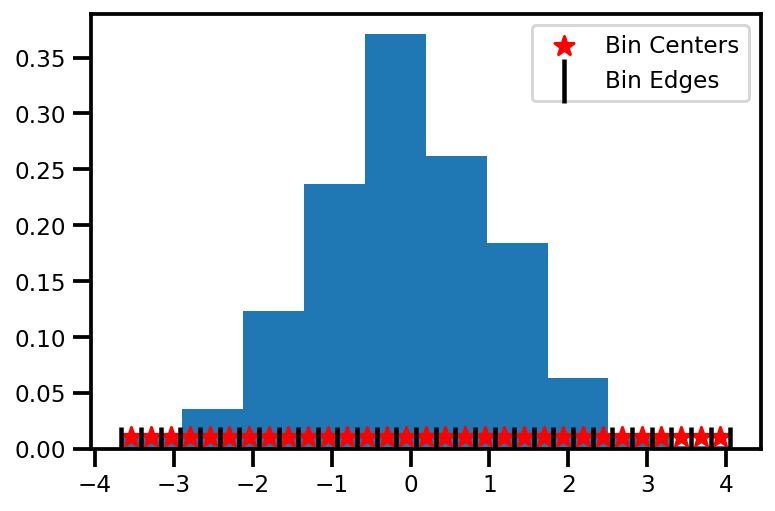
2. Get Bin Centers#
In the numpy implementation, we are only given the bin_edges and we need to bin_centers. It’s a minor thing but it’s important in order to get the width between each of the
# get the bin centers
bin_centers = jnp.mean(jnp.vstack((bin_edges[0:-1], bin_edges[1:])), axis=0)
delta = bin_centers[3] - bin_centers[2]
# visualize
fig, ax = plt.subplots()
ax.hist(data, bins=10, density=True)
ax.scatter(bin_centers, 0.01 * np.ones_like(bin_centers), marker="*", s=100, zorder=4, color='red', label="Bin Centers")
ax.scatter(bin_edges, np.zeros_like(bin_edges), marker="|", s=500, zorder=4, color='black', label="Bin Edges")
plt.legend()
plt.show()
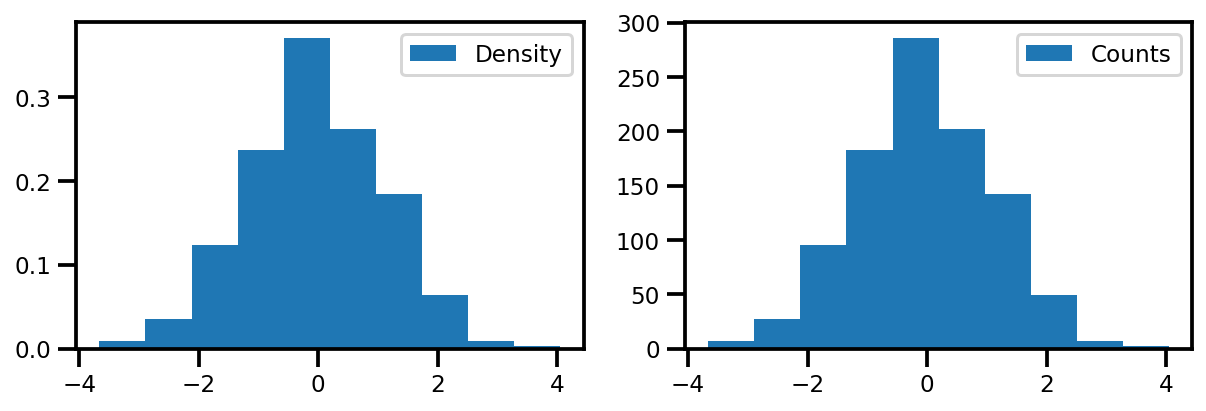
4. Get Normalized Density#
# get the normalized density
pk = 1.0 * jnp.array(counts) / jnp.sum(counts)
fig, ax = plt.subplots(ncols=2, figsize=(10, 3))
ax[0].hist(data, bins=10, density=True)
ax[0].legend(["Density"])
ax[1].hist(data, bins=10, density=False)
ax[1].legend(["Counts"])
plt.show()
5. Calculate Entropy given the probability#
# manually
H = 0.0
for ip_k in pk:
if ip_k > 0.0:
H += - ip_k * jnp.log(ip_k)
H += jnp.log(delta)
# H += np.log(delta)
print(f"MLE Estimator: {H:.4f} nats")
print(f"True Estimator: {H_true:.4f} nats")
MLE Estimator: 1.5379 nats
True Estimator: 1.5448 nats
# refactored
from jax.scipy.special import entr
H_vec = entr(pk)
H_vec = jnp.sum(H_vec)
H_vec += jnp.log(delta)
np.testing.assert_almost_equal(H, H_vec)
Refactor - Scipy#
from scipy.stats import rv_histogram
histogram = np.histogram(data, bins=bins, range=(data_min, data_max), density=False)
hist_dist = rv_histogram(histogram)
H_mle = hist_dist.entropy()
np.testing.assert_almost_equal(H_mle, H_vec, decimal=6)
print(f"Scipy Estimator: {H_mle:.4f} nats")
print(f"My Estimator: {H:.4f} nats")
print(f"True Estimator: {H_true:.4f} nats")
Scipy Estimator: 1.5379 nats
My Estimator: 1.5379 nats
True Estimator: 1.5448 nats
It’s known in the community that this will under estimate the probability distribution.
Resources:
Blog Post - Sebasian Nowozin (2015)
Corrections#
Miller-Maddow#
where \(\hat{m}\) are the number of bins with non-zero \(p_N\) probability.
# get histogram counts
hist_counts = histogram[0]
total_counts = np.sum(hist_counts)
total_nonzero_counts = np.sum(hist_counts > 0)
N = data.shape[0]
# get correction
mm_correction = 0.5 * (np.sum(hist_counts > 0) - 1) / np.sum(hist_counts)
print(mm_correction)
0.0145
total_counts, total_nonzero_counts
(1000, 30)
H_mm = H + mm_correction
print(f"My Estimator:\n{H:.4f} nats")
print(f"Miller-Maddow Estimator:\n{H_mm:.4f} nats")
print(f"True Estimator:\n{H_true:.4f} nats")
My Estimator:
1.5379 nats
Miller-Maddow Estimator:
1.5524 nats
True Estimator:
1.5448 nats
Custom Function#
from chex import Array
from typing import Callable, Tuple, Union
def get_domain_extension(
data: Array, extension: Union[float, int],
) -> Tuple[float, float]:
"""Gets the extension for the support
Parameters
----------
data : Array
the input data to get max and minimum
extension : Union[float, int]
the extension
Returns
-------
lb : float
the new extended lower bound for the data
ub : float
the new extended upper bound for the data
"""
# case of int, convert to float
if isinstance(extension, int):
extension = float(extension / 100)
# get the domain
domain = jnp.abs(jnp.max(data) - jnp.min(data))
# extend the domain
domain_ext = extension * domain
# get the extended domain
lb = jnp.min(data) - domain_ext
up = jnp.max(data) + domain_ext
return lb, up
def histogram_jax_entropy(data: Array, bin_est_f: Callable, extension: Union[float, int]=10):
# get extension
lb, ub = get_domain_extension(data, extension)
# histogram bin width
bin_width = bin_est_f(data)
# histogram bins
nbins = get_num_bins(data, bin_width, lb, ub)
# histogram
counts, bin_edges = jnp.histogram(data, bins=nbins, density=False)
# get the normalized density
pk = 1.0 * jnp.array(counts) / jnp.sum(counts)
# get delta
delta = bin_edges[3] - bin_edges[2]
# calculate entropy
H = entr(pk)
H = jnp.sum(H)
H += jnp.log(delta)
return H
from chex import Array
import math
def hist_bin_scott(x: Array) -> Array:
"""Optimal histogram bin width based on scotts method.
Uses the 'normal reference rule' which assumes the data
is Gaussian
Parameters
----------
x : Array
The input array, (n_samples)
Returns
-------
bin_width : Array
The optimal bin width, ()
"""
n_samples = x.shape[0]
# print(3.5 * np.std(x) / (n_samples ** (1/3)))
return (24.0 * math.pi ** 0.5 / n_samples) ** (1.0 / 3.0) * jnp.std(x)
def get_num_bins(data, bin_width, data_min, data_max):
nbins = jnp.ceil((data_max - data_min) / bin_width)
nbins = jnp.maximum(1, nbins).astype(jnp.int32)
bins = data_min + bin_width * jnp.arange(0, nbins+1, 1)
return nbins
import jax.numpy as jnp
from jax.scipy.special import entr
def histogram_entropy(data, bins=None):
"""Estimate univariate entropy with a histogram
Notes
-----
* uses scott's method
* entropy is in nats
"""
# histogram bin width (scotts)
bin_width = 3.5 * jnp.std(data) / (data.shape[0] ** (1/3))
if bins is None:
# histogram bins
nbins = jnp.ceil((data.max() - data.min()) / bin_width)
nbins = nbins.astype(jnp.int32)
# get bins with linspace
bins = jnp.linspace(data.min(), data.max(), nbins)
# # bins with arange (similar to astropy)
# bins = data_min + bin_width * jnp.arange(0, nbins+1, 1)
# histogram
counts, bin_edges = jnp.histogram(data, bins=bins, density=False)
# normalized the bin counts for a density
pk = 1.0 * jnp.array(counts) / jnp.sum(counts)
# calculate entropy
H = entr(pk)
H = jnp.sum(H)
# add correction for continuous case
delta = bin_edges[3] - bin_edges[2]
H += jnp.log(delta)
return H
import numpy as np
import jax
data = np.random.randn(1_000)
data = jnp.array(data, dtype=jnp.float32)
histogram_entropy(jnp.array(data).ravel(), 10)
DeviceArray(1.4400792, dtype=float32)
f = jax.jit(jax.partial(histogram_entropy, bins=None))
f(data.ravel())
---------------------------------------------------------------------------
FilteredStackTrace Traceback (most recent call last)
<ipython-input-23-a151071957d4> in <module>
2
----> 3 f(data.ravel())
<ipython-input-20-58a03409a594> in histogram_entropy(data, bins)
20 # get bins with linspace
---> 21 bins = jnp.linspace(data.min(), data.max(), nbins)
22
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/_src/numpy/lax_numpy.py in linspace(start, stop, num, endpoint, retstep, dtype, axis)
3094 lax._check_user_dtype_supported(dtype, "linspace")
-> 3095 num = core.concrete_or_error(operator.index, num, "'num' argument of jnp.linspace")
3096 axis = core.concrete_or_error(operator.index, axis, "'axis' argument of jnp.linspace")
FilteredStackTrace: jax._src.errors.ConcretizationTypeError: Abstract tracer value encountered where concrete value is expected: Traced<ShapedArray(int32[])>with<DynamicJaxprTrace(level=0/1)>
'num' argument of jnp.linspace
While tracing the function histogram_entropy at <ipython-input-20-58a03409a594>:4, this concrete value was not available in Python because it depends on the value of the arguments to histogram_entropy at <ipython-input-20-58a03409a594>:4 at flattened positions [0], and the computation of these values is being staged out (that is, delayed rather than executed eagerly).
(https://jax.readthedocs.io/en/latest/errors.html#jax.errors.ConcretizationTypeError)
The stack trace above excludes JAX-internal frames.
The following is the original exception that occurred, unmodified.
--------------------
The above exception was the direct cause of the following exception:
ConcretizationTypeError Traceback (most recent call last)
<ipython-input-23-a151071957d4> in <module>
1 f = jax.jit(jax.partial(histogram_entropy, bins=None))
2
----> 3 f(data.ravel())
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/_src/traceback_util.py in reraise_with_filtered_traceback(*args, **kwargs)
137 def reraise_with_filtered_traceback(*args, **kwargs):
138 try:
--> 139 return fun(*args, **kwargs)
140 except Exception as e:
141 if not is_under_reraiser(e):
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/api.py in f_jitted(*args, **kwargs)
405 return cache_miss(*args, **kwargs)[0] # probably won't return
406 else:
--> 407 return cpp_jitted_f(*args, **kwargs)
408
409 f_jitted._cpp_jitted_f = cpp_jitted_f
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/api.py in cache_miss(*args, **kwargs)
293 _check_arg(arg)
294 flat_fun, out_tree = flatten_fun(f, in_tree)
--> 295 out_flat = xla.xla_call(
296 flat_fun,
297 *args_flat,
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/core.py in bind(self, fun, *args, **params)
1400
1401 def bind(self, fun, *args, **params):
-> 1402 return call_bind(self, fun, *args, **params)
1403
1404 def process(self, trace, fun, tracers, params):
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/core.py in call_bind(primitive, fun, *args, **params)
1391 tracers = map(top_trace.full_raise, args)
1392 with maybe_new_sublevel(top_trace):
-> 1393 outs = primitive.process(top_trace, fun, tracers, params)
1394 return map(full_lower, apply_todos(env_trace_todo(), outs))
1395
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/core.py in process(self, trace, fun, tracers, params)
1403
1404 def process(self, trace, fun, tracers, params):
-> 1405 return trace.process_call(self, fun, tracers, params)
1406
1407 def post_process(self, trace, out_tracers, params):
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/core.py in process_call(self, primitive, f, tracers, params)
598
599 def process_call(self, primitive, f, tracers, params):
--> 600 return primitive.impl(f, *tracers, **params)
601 process_map = process_call
602
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/interpreters/xla.py in _xla_call_impl(fun, device, backend, name, donated_invars, *args)
575
576 def _xla_call_impl(fun: lu.WrappedFun, *args, device, backend, name, donated_invars):
--> 577 compiled_fun = _xla_callable(fun, device, backend, name, donated_invars,
578 *unsafe_map(arg_spec, args))
579 try:
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/linear_util.py in memoized_fun(fun, *args)
258 fun.populate_stores(stores)
259 else:
--> 260 ans = call(fun, *args)
261 cache[key] = (ans, fun.stores)
262
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/interpreters/xla.py in _xla_callable(fun, device, backend, name, donated_invars, *arg_specs)
652 abstract_args, arg_devices = unzip2(arg_specs)
653 if config.omnistaging_enabled:
--> 654 jaxpr, out_avals, consts = pe.trace_to_jaxpr_final(fun, abstract_args)
655 if any(isinstance(c, core.Tracer) for c in consts):
656 raise core.UnexpectedTracerError("Encountered an unexpected tracer.")
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/interpreters/partial_eval.py in trace_to_jaxpr_final(fun, in_avals)
1226 main.source_info = fun_sourceinfo(fun.f) # type: ignore
1227 main.jaxpr_stack = () # type: ignore
-> 1228 jaxpr, out_avals, consts = trace_to_subjaxpr_dynamic(fun, main, in_avals)
1229 del fun, main
1230 return jaxpr, out_avals, consts
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/interpreters/partial_eval.py in trace_to_subjaxpr_dynamic(fun, main, in_avals)
1206 trace = DynamicJaxprTrace(main, core.cur_sublevel())
1207 in_tracers = map(trace.new_arg, in_avals)
-> 1208 ans = fun.call_wrapped(*in_tracers)
1209 out_tracers = map(trace.full_raise, ans)
1210 jaxpr, out_avals, consts = frame.to_jaxpr(in_tracers, out_tracers)
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/linear_util.py in call_wrapped(self, *args, **kwargs)
164
165 try:
--> 166 ans = self.f(*args, **dict(self.params, **kwargs))
167 except:
168 # Some transformations yield from inside context managers, so we have to
<ipython-input-20-58a03409a594> in histogram_entropy(data, bins)
19
20 # get bins with linspace
---> 21 bins = jnp.linspace(data.min(), data.max(), nbins)
22
23 # # bins with arange (similar to astropy)
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/_src/numpy/lax_numpy.py in linspace(start, stop, num, endpoint, retstep, dtype, axis)
3093 """Implementation of linspace differentiable in start and stop args."""
3094 lax._check_user_dtype_supported(dtype, "linspace")
-> 3095 num = core.concrete_or_error(operator.index, num, "'num' argument of jnp.linspace")
3096 axis = core.concrete_or_error(operator.index, axis, "'axis' argument of jnp.linspace")
3097 if num < 0:
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/core.py in concrete_or_error(force, val, context)
966 return force(val.aval.val)
967 else:
--> 968 raise ConcretizationTypeError(val, context)
969 else:
970 return force(val)
ConcretizationTypeError: Abstract tracer value encountered where concrete value is expected: Traced<ShapedArray(int32[])>with<DynamicJaxprTrace(level=0/1)>
'num' argument of jnp.linspace
While tracing the function histogram_entropy at <ipython-input-20-58a03409a594>:4, this concrete value was not available in Python because it depends on the value of the arguments to histogram_entropy at <ipython-input-20-58a03409a594>:4 at flattened positions [0], and the computation of these values is being staged out (that is, delayed rather than executed eagerly).
(https://jax.readthedocs.io/en/latest/errors.html#jax.errors.ConcretizationTypeError)
Bin Width#
def get_bins(data, bin_width, data_min, data_max):
nbins = jnp.ceil((data_max - data_min) / bin_width)
nbins = jnp.maximum(1, nbins)
bins = jnp.linspace(data_min, data_max, nbins+1)
# bins = data_min + bin_width * jnp.arange(start=0.0, stop=nbins + 1)
return bins
nbins = jnp.ceil((data_max - data_min) / bin_width)
nbins = jnp.maximum(1, nbins)
print(nbins)
# data_min + bin_wijnp.arange(start=0.0, stop=nbins+1)
17.0
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-143-a07b0a52ebca> in <module>
2 nbins = jnp.maximum(1, nbins)
3 print(nbins)
----> 4 data_min + bin_wijnp.arange(start=0.0, stop=nbins+1)
NameError: name 'bin_wijnp' is not defined
def get_histogram_entropy(data, bins):
histogram = jnp.histogram(data, bins=bins,density=False)
hist_dist = rv_histogram(histogram)
H_mle = hist_dist.entropy()
print(f"MLE Estimator: {H_mle:.4f} nats")
bins = get_bins(data, 0.5, data_min, data_max)
get_histogram_entropy(data, bins)
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-141-c9c88f7d4eb0> in <module>
----> 1 bins = get_bins(data, 0.5, data_min, data_max)
2
3
4 get_histogram_entropy(data, bins)
<ipython-input-139-ff3a1bcbc6e5> in get_bins(data, bin_width, data_min, data_max)
2 nbins = jnp.ceil((data_max - data_min) / bin_width)
3 nbins = jnp.maximum(1, nbins).astype(jnp.float32)
----> 4 bins = jnp.linspace(data_min, data_max, nbins+1)
5 # bins = data_min + bin_width * jnp.arange(start=0.0, stop=nbins + 1)
6 return bins
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/_src/numpy/lax_numpy.py in linspace(start, stop, num, endpoint, retstep, dtype, axis)
3093 """Implementation of linspace differentiable in start and stop args."""
3094 lax._check_user_dtype_supported(dtype, "linspace")
-> 3095 num = core.concrete_or_error(operator.index, num, "'num' argument of jnp.linspace")
3096 axis = core.concrete_or_error(operator.index, axis, "'axis' argument of jnp.linspace")
3097 if num < 0:
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/core.py in concrete_or_error(force, val, context)
968 raise ConcretizationTypeError(val, context)
969 else:
--> 970 return force(val)
971
972 convert_element_type_p = Primitive('convert_element_type')
~/.conda/envs/jax_py38/lib/python3.8/site-packages/jax/interpreters/xla.py in _forward_method(attrname, self, fun, *args)
1010
1011 def _forward_method(attrname, self, fun, *args):
-> 1012 return fun(getattr(self, attrname), *args)
1013 _forward_to_value = partial(_forward_method, "_value")
1014
TypeError: only integer scalar arrays can be converted to a scalar index
Scotts#
where \(\sigma\) is the standard deviation and \(n\) is the number of samples.
from chex import Array
import math
def hist_bin_scott(x: Array) -> Array:
"""Optimal histogram bin width based on scotts method.
Uses the 'normal reference rule' which assumes the data
is Gaussian
Parameters
----------
x : Array
The input array, (n_samples)
Returns
-------
bin_width : Array
The optimal bin width, ()
"""
n_samples = x.shape[0]
# print(3.5 * np.std(x) / (n_samples ** (1/3)))
return (24.0 * math.pi ** 0.5 / n_samples) ** (1.0 / 3.0) * jnp.std(x)
bin_width = hist_bin_scott(data)
bins = get_bins(data, bin_width, data_min, data_max)
get_histogram_entropy(data, bins)
MLE Estimator: 1.6740 nats
Freedman#
def hist_bin_freedman(x: Array) -> Array:
"""Optimal histogram bin width based on scotts method.
Uses the 'normal reference rule' which assumes the data
is Gaussian
Parameters
----------
x : Array
The input array, (n_samples)
Returns
-------
bin_width : Array
The optimal bin width, ()
"""
n_samples = x.shape[0]
# print(3.5 * np.std(x) / (n_samples ** (1/3)))
return (24.0 * math.pi ** 0.5 / n_samples) ** (1.0 / 3.0) * jnp.std(x)
Silverman#
Gaussian#
#
Volume#
def volume_unit_ball(d_dimensions: int, norm=2) -> float:
"""Volume of the unit l_p-ball in d-dimensional
Parameters
----------
d_dimensions : int
Number of dimensions to estimate the volume
norm : int, default=2
The type of ball to get the volume.
* 2 : euclidean distance
* 1 : manhattan distance
* 0 : chebyshev distance
Returns
-------
vol : float
The volume of the d-dimensional unit ball
References
----------
[1]: Demystifying Fixed k-Nearest Neighbor Information
Estimators - Gao et al (2016)
"""
# get ball
if norm == 0:
return 1.0
elif norm == 1:
raise NotImplementedError()
elif norm == 2:
b = 2.0
else:
raise ValueError(f"Unrecognized norm: {norm}")
numerator = gamma(1.0 + 1.0 / b) ** d_dimensions
denomenator = gamma(1.0 + d_dimensions / b)
vol = 2 ** d_dimensions * numerator / denomenator
return vol

