Generative Models#
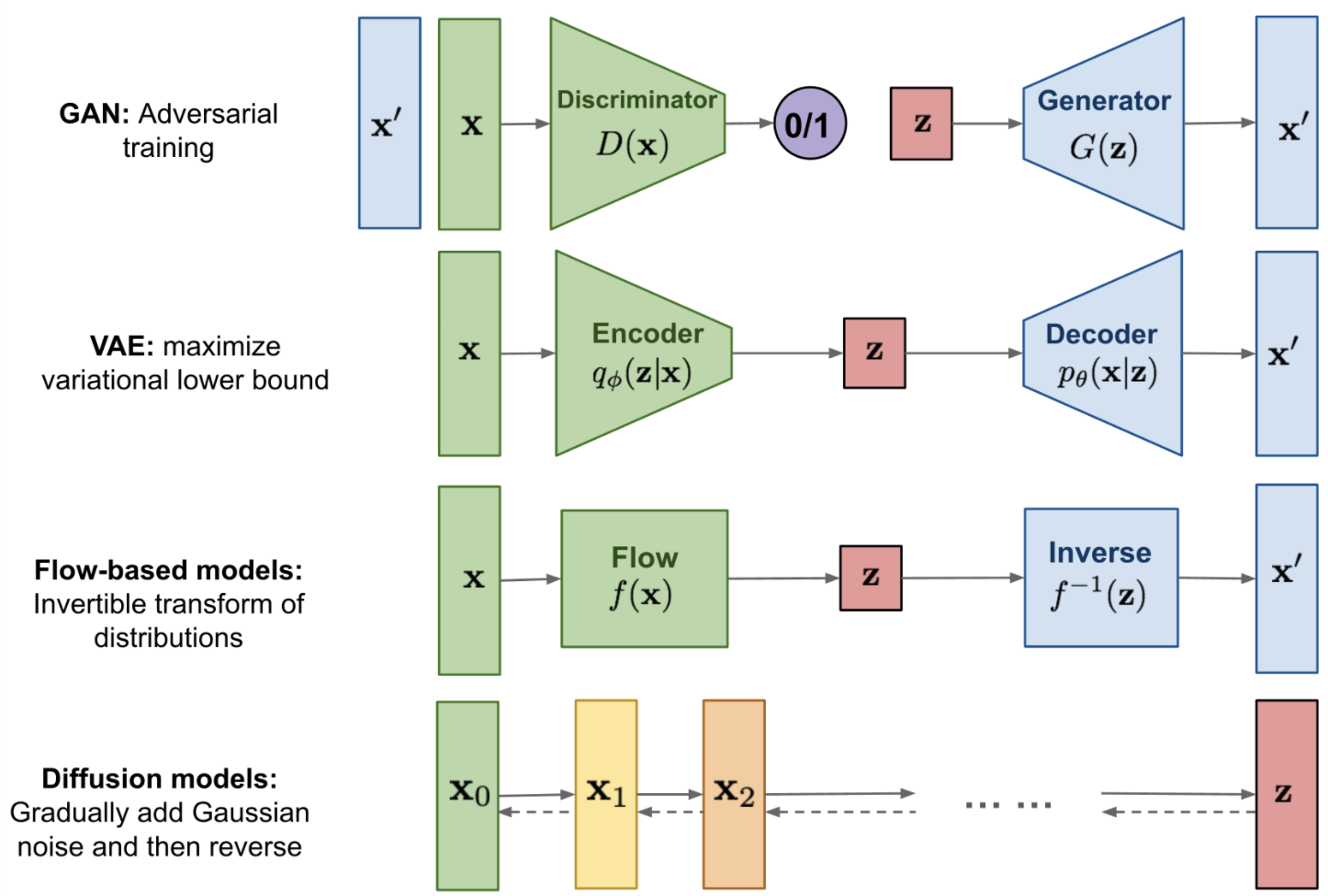
Fig. 10 This figure was taken from Lilians blog.#
\[
p(x,z) = p(x,z)p(z)
\]
Quantities of Interest#
By having this generative model, we are typically only interested in two things: sampling and density estimation.
Sampling#
We want to be able to generate samples of, \(x'\), such that they are indistinguishable from our real data distribution, \(x\).
\[
x' \sim P_X(\boldsymbol{\theta})
\]
Density Estimation#
We want to be able to estimate densities of new data samples
\[
p(x; \boldsymbol{\theta})
\]
Recipes#
Generate samples from the latent variable.
\[
z' \sim P_Z
\]
Propagate the samples through the transformation
\[
x' = T(z'; \boldsymbol{\theta})
\]
Latent Variable#
We generally require this to be simple as possible:
Gaussian#
\[
z \sim \mathcal{N}(0, 1)
\]
Uniform#
\[
z \sim \mathcal{U}([0,1])
\]
Mixture of Distributions#
Models#

Fig. 11 Overview of generative models. Source: [Weng, 2021].#
