QG PDE#
Assumptions#
Representation#
We have a coordinate vector, \(\mathbf{x} \in \mathbb{R}^D\), which describe the state 2D space \((x,y)\). We also have a time component, \(t\), which describes the 2D space at a specific point in time. We also have a two functions which describe the flow state: the potential function, \(\boldsymbol{q}\), is the … and the \(\boldsymbol{\psi}\) is an auxilary function which …. Both functions take in the coordinate vector and time and output a scalar value.
PDE#
We have the following PDE for the QG dynamics:
where \(q(x,t) \in \mathbb{R}^2 \times \mathbb{R} \rightarrow \mathbb{R}\) is the potential vorticity (PV), \(\psi(x,t) \in \mathbb{R}^2 \times \mathbb{R} \rightarrow \mathbb{R}\) is the stream function, \(\partial_t\) is the partial derivative wrt \(t\), \(\boldsymbol{J}\), is the Jacobian operator and \(\det \boldsymbol{J}(\cdot,\cdot)\) is the determinant of the Jacobian.
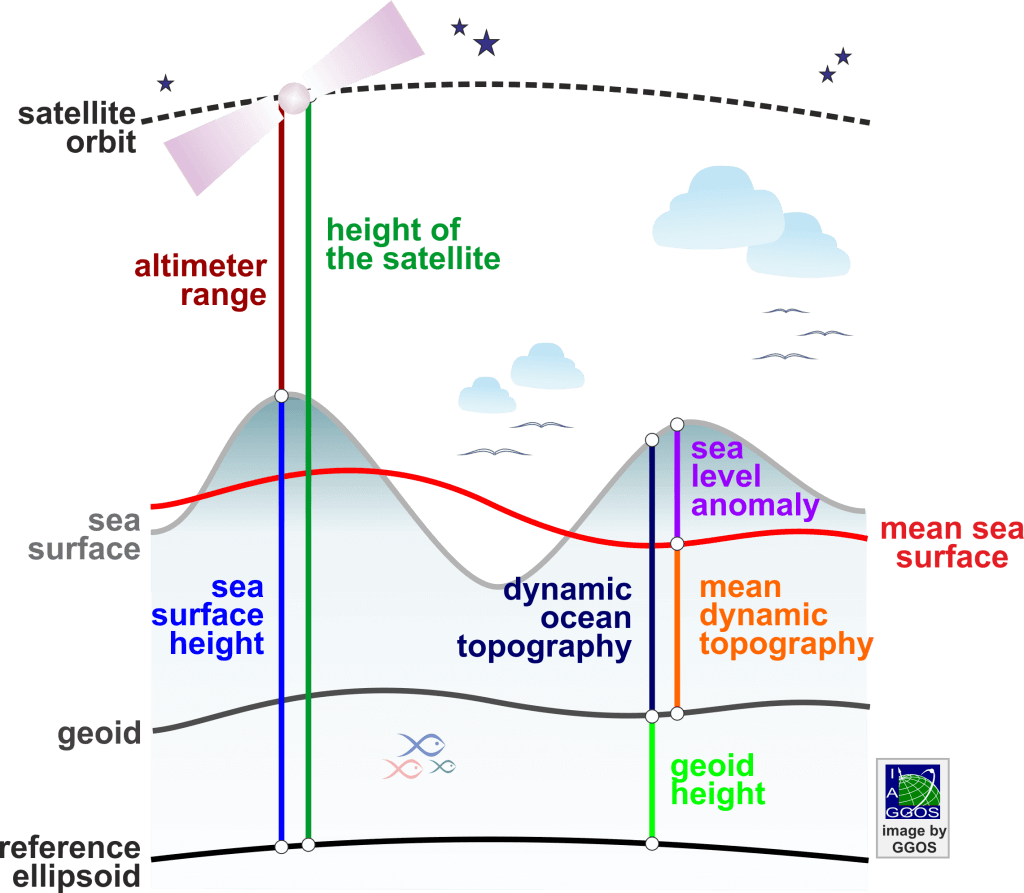
Objective: We want to convert this PDE in terms of sea surface height (SSH) instead of PV and the stream function.
PINNs Loss Derivation#
Stream Function#
Let’s define the relationship between the SSH, \(u\), and the stream function \(\psi\).
where \(c_1 = \frac{f}{g}\). If we plug in the SSH into the PDE, we get:
To simplify the notation, we will factor out the constant, \(c_1\), from the determinant Jacobian term.
Proof: Constants and determinant Jacobians#
Note: we used the property that \(\partial (c f) = c \partial f\).
QED.
Potential Vorticity#
Now, let’s define the relationship between the stream function and the PV. This is given by:
where \(\nabla^2\) is the Laplacian operator and \(c_2 = \frac{1}{L_R^2}\). If we plug in SSH, \(u\), into the stream function, as defined above, we get:
where \(c_3 = c_1 c_2 = \frac{f}{g L_R^2}\). We can plug in the PV, \(q\), into the PDE in terms of SSH, \(u\).
Now, we can expand this equation but first let’s break this up into two terms:
Now we will tackle both of these terms one at a time.
Term I
So term I is:
We can expand this via the partial derivative, \(\partial_t\).
So plugging this back into the PDE gives us:
Term II
We can factorize this determinant Jacobian term.
And furthermore, we can factor out the constants
Proof: Determinant Jacobian Expansion#
So term II is:
We know the definition of the determinant of the Jacobian for a vector-valued function, \(\boldsymbol{f} = [f_1(x,y), f_2(x,y)]^\top: \mathbb{R}^2 \rightarrow \mathbb{R}^2\), as there is an identity.
If use this identity with term II, we get:
Again, let’s split this up into two subterms and tackle them one-by-one.
Term IIa
We have the following term for Term IIa:
We can expand the terms to get the following:
And we can simplify, by factoring out constants, to get:
Term IIb
We can expand the terms to get the following:
Combined (Term IIa, IIb)
We can substitute all of these two terms into our original expression
If we group the terms by operators, \(\partial, \nabla^2\), then we get:
So each of these terms are determinant Jacobian terms, \(\det \boldsymbol J\).
We have the final form for our PDE in terms of SSH, \(u\), which combines terms I and II.
QED.
Final Form#
So we have the final form for our PDE in terms of SSH.
We will factor out a constant term
Expanded Form#
It is also good to do the expanded form with all of the partial derivatives because then we can see the computational portions with the gradient operations.
Again, we will group the terms together in terms of the order of their derivatives, \((\nabla^2, \partial)\).
Now, another grouping:
QG Equation (SSH)#
Note: For the ease of notation, let’s denote \(u\) as the SSH. The above PDE can be written in terms of \(u\)
Note: See derivation for how I came up with this term.
Expanded Form#
We will do the expanded form with all of the partial derivatives so that we can see the gradient operations which we will need for the computational portions.
Again, we will group the terms together in terms of the order of their derivatives, \((\nabla^2, \partial)\).
Now, another grouping:
Now, we will use the expanded forms to do the code. I have snippets using PyTorch and Jax (TODO). They use the DAG/OOP and Functional approach (respectively) so the notation is slightly different.
Gradient (1st Order)#
Let’s look at the first-order gradients.
Code#
Let’s use the following notation:
where \(\mathbf{x} \in \mathbb{R}^D\), \(\mathbf{u} \in \mathbb{R}\), and \(D = [N_x, N_y, N_t]\).
Note: This is the PyTorch notation.
# coords variable, (B, D)
x = torch.Variable(x, requires_grad=True)
# output variable, (B,)
u = model(x)
# Jacobian vector, (B, D)
u_jac = jacobian(u, x)
# partial derivatives, (B,)
u_x, u_y, u_t = split(u_jac, dim=1)
# calculate term 2, (B,)
term2 = c2 * u_t + c3 * u_x * u_y - c3 * u_y * u_x
Laplacian + Gradient#
Now we can look at the second order gradients.
Note: This is where all of the computational expense will come from.
Code#
# coords variable, (B, D)
x = torch.Variable(x, requires_grad=True)
# output variable, (B,)
u = model(x)
# Laplacian (B,)
u_lap = laplacian(u, x)
# gradient of laplacian, (B, D)
u_lap_jac = jacobian(u_lap, x)
# partial derivatives, (B,)
u_lap_x, u_lap_y, u_lap_t = split(u_lap_jac, dim=1)
# calculate term
term1 = u_lap_t + c1 * u_x * u_lap_y - c1 * u_y * u_lap_x
Althernative (cheaper?)
We can also try this re-using the gradients we have already computed (from term 1). This will reduce the computations a bit by reusing our previous jacobian calculation to remove recalculating the Laplacian.
# coords variable, (B, D)
x = torch.Variable(x, requires_grad=True)
# output variable, (B,)
u = model(x)
# Jacobian vector, (B, D)
u_jac = jacobian(u, x)
u_jac2 = jacobian(u_jac, x)
u_xx, u_yy, u_tt = split(u_jac2, dim=1)
# Laplacian (B,)
u_lap = u_xx + u_yy
# gradient of laplacian, (B, D)
u_lap_jac = jacobian(u_lap, x)
# partial derivatives, (B,)
u_lap_x, u_lap_y, u_lap_t = split(u_lap_jac, dim=1)
# calculate term
term1 = u_lap_t + c1 * u_x * u_lap_y - c1 * u_y * u_lap_x
Loss#
So now we combine both losses to get the full loss.
Note: We typically square this term. It helps during the minimization process to always have a positive value. Otherwise, it will try to minimize a negative value. Instead of the squared term, we can also do the absolute value or perhaos the square root of the squared term.
# (B,)
term_partial = ...
# (B,)
term_nabla = ...
# combine terms
loss = term_partial + term_nabla
# compute loss term
loss = loss.square().mean()
# scale the loss
loss *= alpha
My Code#
You can find the full function here. I have included the full function below for anyone interested.
# from ..operators.differential_simp import gradient
from ..operators.differential import grad as gradient
import torch
import torch.nn as nn
class QGRegularization(nn.Module):
def __init__(
self, f: float = 1e-4, g: float = 9.81, Lr: float = 1.0, reduction: str = "mean"
):
super().__init__()
self.f = f
self.g = g
self.Lr = Lr
self.reduction = reduction
def forward(self, out, x):
x = x.requires_grad_(True)
# gradient, nabla x
out_jac = gradient(out, x)
assert out_jac.shape == x.shape
# calculate term 1
loss1 = _qg_term1(out_jac, x, self.f, self.g, self.Lr)
# calculate term 2
loss2 = _qg_term2(out_jac, self.f, self.g, self.Lr)
loss = (loss1 + loss2).sq
if self.reduction == "sum":
return loss.sum()
elif self.reduction == "mean":
return loss.mean()
else:
raise ValueError(f"Unrecognized reduction: {self.reduction}")
def qg_constants(f, g, L_r):
c_1 = f / g
c_2 = 1 / L_r**2
c_3 = c_1 * c_2
return c_1, c_2, c_3
def qg_loss(
ssh, x, f: float = 1e-4, g: float = 9.81, Lr: float = 1.0, reduction: str = "mean"
):
# gradient, nabla x
# x = x.detach().clone().requires_grad_(True)
# print(x.shape, ssh.shape)
ssh_jac = gradient(ssh, x)
assert ssh_jac.shape == x.shape
# calculate term 1
loss1 = _qg_term1(ssh_jac, x, f, g, Lr)
# calculate term 2
loss2 = _qg_term2(ssh_jac, f, g, Lr)
loss = torch.sqrt((loss1 + loss2) ** 2)
if reduction == "sum":
return loss.sum()
elif reduction == "mean":
return loss.mean()
else:
raise ValueError(f"Unrecognized reduction: {reduction}")
def _qg_term1(u_grad, x_var, f: float = 1.0, g: float = 1.0, L_r: float = 1.0):
"""
t1 = ∂𝑡∇2𝑢 + 𝑐1 ∂𝑥𝑢 ∂𝑦∇2𝑢 − 𝑐1 ∂𝑦𝑢 ∂𝑥∇2𝑢
Parameters:
----------
u_grad: torch.Tensor, (B, Nx, Ny, T)
x_var: torch.Tensor, (B,
f: float, (,)
g: float, (,)
Lr: float, (,)
Returns:
--------
loss : torch.Tensor, (B,)
"""
x_var = x_var.requires_grad_(True)
c_1, c_2, c_3 = qg_constants(f, g, L_r)
# get partial derivatives | partial x, y, t
u_x, u_y, u_t = torch.split(u_grad, [1, 1, 1], dim=1)
# jacobian^2 x2, ∇2
u_grad2 = gradient(u_grad, x_var)
assert u_grad2.shape == x_var.shape
# split jacobian -> partial x, partial y, partial t
u_xx, u_yy, u_tt = torch.split(u_grad2, [1, 1, 1], dim=1)
assert u_xx.shape == u_yy.shape == u_tt.shape
# laplacian (spatial), nabla^2
u_lap = u_xx + u_yy
assert u_lap.shape == u_xx.shape == u_yy.shape
# gradient of laplacian, ∇ ∇2
u_lap_grad = gradient(u_lap, x_var)
assert u_lap_grad.shape == x_var.shape
# split laplacian into partials
u_lap_grad_x, u_lap_grad_y, u_lap_grad_t = torch.split(u_lap_grad, [1, 1, 1], dim=1)
assert u_lap_grad_x.shape == u_lap_grad_y.shape == u_lap_grad_t.shape
# term 1
loss = u_lap_grad_t + c_1 * u_x * u_lap_grad_y - c_1 * u_y * u_lap_grad_x
assert loss.shape == u_lap_grad_t.shape == u_lap_grad_y.shape == u_lap_grad_x.shape
return loss
def _qg_term2(u_grad, f: float = 1.0, g: float = 1.0, Lr: float = 1.0):
"""
t2 = 𝑐2 ∂𝑡(𝑢) + 𝑐3 ∂𝑥(𝑢) ∂𝑦(𝑢) − 𝑐3 ∂𝑦(𝑢) ∂𝑥(𝑢)
Parameters:
----------
ssh_grad: torch.Tensor, (B, Nx, Ny, T)
f: float, (,)
g: float, (,)
Lr: float, (,)
Returns:
--------
loss : torch.Tensor, (B,)
"""
_, c_2, c_3 = qg_constants(f, g, Lr)
# get partial derivatives | partial x, y, t
u_x, u_y, u_t = torch.split(u_grad, [1, 1, 1], dim=1)
# calculate term 2
loss = c_2 * u_t + c_3 * u_x * u_y - c_3 * u_y * u_x
return loss
Previous Code#
Redouane#
He previously made some attempts to use this as a regularization term. Here is his code snippet.
def forward(self, coords):
coords = coords.clone().detach().requires_grad_(True) # allows to take derivative w.r.t. input
SSH = self.firstnet(coords)
gradSSH = self.gradient(SSH, coords)
dSSHdx = gradSSH[:,0:1]
dSSHdy = gradSSH[:,1:2]
d2SHHd2x = self.gradient(dSSHdx, coords)[:,0:1]
d2SHHd2y = self.gradient(dSSHdy, coords)[:,1:2]
dQ = self.gradient(d2SHHd2x+d2SHHd2y, coords)
output = self.secondnet(self.Bnorm(torch.cat((dSSHdy,
dSSHdx,
d2SHHd2x+d2SHHd2y,
dQ[:,0:1],
dQ[:,1:2]),1)))
#dQ[:,0:1] * dSSHdy,
#dQ[:,1:2] * dSSHdx
output = dSSHdx * dQ[:,1:2] - dSSHdy * dQ[:,0:1]
return (1e-5*dQ[:,2:3]-output), coords, SSH
